
【题目】在无穷数列![]() 中,
中, ![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
, ![]() .设
.设![]() ,记使得
,记使得![]() 成立的n的最大值为
成立的n的最大值为![]() .
.
(Ⅰ)设数列{an}为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{an}为等比数列,且a2=2,求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,求出所有可能的数列{an}.
【答案】(Ⅰ)b1=1, b2=1, b3=2;(Ⅱ)243;(Ⅲ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意结合数列![]() 的定义可得b1=1, b2=1, b3=2.
的定义可得b1=1, b2=1, b3=2.
(Ⅱ)由题意可得![]() ,则b1=1,b2=b3=2,b4=b5= b6= b7=3,b8=b9
,则b1=1,b2=b3=2,b4=b5= b6= b7=3,b8=b9![]() b15=4,b16=b17
b15=4,b16=b17![]() b31=5,b32=b33
b31=5,b32=b33![]() b50= 6.故b1+ b2+b3
b50= 6.故b1+ b2+b3![]() b50=243.
b50=243.
(Ⅲ)由题意可知![]() .使得
.使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,使得
,使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,则
,则![]() .结合题中的条件分析可得
.结合题中的条件分析可得![]() ,故
,故![]() .
.
试题解析:
(Ⅰ)b1=1, b2=1, b3=2.
(Ⅱ)因为![]() 为等比数列, a1=1,a2=2,
为等比数列, a1=1,a2=2,
所以![]() ,
,
因为使得an≤m成立的n的最大值为bm,
所以b1=1,b2=b3=2,b4=b5= b6= b7=3,b8=b9![]() b15=4,b16=b17
b15=4,b16=b17![]() b31=5,b32=b33
b31=5,b32=b33![]() b50= 6.故b1+ b2+b3
b50= 6.故b1+ b2+b3![]() b50=243.所以b1+ b2+b3+…b50=243.
b50=243.所以b1+ b2+b3+…b50=243.
(Ⅲ)由题意,得![]() ,
,
结合条件![]() ,得
,得![]() .
.
又因为使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,使得
,使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,所以
,所以![]() ,
, ![]() .设
.设![]() ,则
,则![]() .
.
假设![]() ,即
,即![]() ,则当
,则当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() ,
, ![]() .
.
因为![]() 为等差数列,所以公差
为等差数列,所以公差![]() ,所以
,所以![]() ,其中
,其中![]() .
.
这与![]() (
(![]() )矛盾,所以
)矛盾,所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
由![]() 为等差数列,得
为等差数列,得![]() ,其中
,其中![]() .
.
因为使得![]() ,由
,由![]() ,
,
得![]() .
.
(1)本题解题的关键是抓住新定义中使得![]() 成立的n的最大值为
成立的n的最大值为![]() ,可将问题迎刃而解.
,可将问题迎刃而解.
(2)对于这类问题,我们首先应弄清问题的本质,然后根据等差数列、等比数列的性质以及解决数列问题时常用的方法即可解决.


科目:高中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(1)求证:AB⊥平面AEC′;
(2)当四棱锥C′﹣ABFE体积取最大值时,
①若G为BC′中点,求异面直线GF与AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.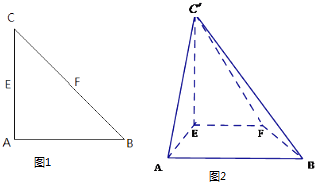
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列结论的证法,再解决后面的问题:
已知 ![]() ,求证:
,求证: ![]() .
.
【证明】构造函数 ![]() ,则
,则 ![]() ,
,
因为对一切 ![]() ,恒有
,恒有 ![]() .
.
所以 ![]() ,从而得
,从而得 ![]() .
.
(1)若 ![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了 ![]() 名女性或
名女性或 ![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.
(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过 ![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
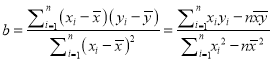 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由直线![]() 的斜率为
的斜率为![]() ,可得所求直线的斜率为
,可得所求直线的斜率为![]() ,代入点斜式方程,可得答案;(2)直线
,代入点斜式方程,可得答案;(2)直线![]() 与两坐标轴的交点分别为
与两坐标轴的交点分别为![]() ,则所围成的三角形的面积为
,则所围成的三角形的面积为![]() ,根据直线
,根据直线![]() 与两坐标轴所围成的三角形的面积为大于
与两坐标轴所围成的三角形的面积为大于![]() ,构造不等式,解得答案.
,构造不等式,解得答案.
试题解析:(1)与直线l垂直的直线的斜率为-2,
因为点(2,3)在该直线上,所以所求直线方程为y-3=-2(x-2),
故所求的直线方程为2x+y-7=0.
(2) 直线l与两坐标轴的交点分别为(-2m+2,0),(0,m-1),
则所围成的三角形的面积为![]() ×|-2m+2|×|m-1|.
×|-2m+2|×|m-1|.
由题意可知![]() ×|-2m+2|×|m-1|>4,化简得(m-1)2>4,
×|-2m+2|×|m-1|>4,化简得(m-1)2>4,
解得m>3或m<-1,
所以实数m的取值范围是(-∞,-1)∪(3,+∞).
【方法点睛】本题主要考查直线的方程,两条直线平行与斜率的关系,属于简单题. 对直线位置关系的考查是热点命题方向之一,这类问题以简单题为主,主要考查两直线垂直与两直线平行两种特殊关系:在斜率存在的前提下,(1)![]() ;(2)
;(2)![]() ,这类问题尽管简单却容易出错,特别是容易遗忘斜率不存在的情况,这一点一定不能掉以轻心.
,这类问题尽管简单却容易出错,特别是容易遗忘斜率不存在的情况,这一点一定不能掉以轻心.
【题型】解答题
【结束】
18
【题目】在平面直角坐标系![]() 中,已知经过原点O的直线
中,已知经过原点O的直线![]() 与圆
与圆![]() 交于
交于![]() 两点。
两点。
(1)若直线![]() 与圆
与圆![]() 相切,切点为B,求直线
相切,切点为B,求直线![]() 的方程;
的方程;
(2)若![]() ,求直线
,求直线![]() 的方程;
的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有2个白球和n(n≥2,n ![]() N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
(I)用含n的代数式表示1次摸球中奖的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;
(III)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com