
【题目】已知椭圆![]() :
:![]()
![]() 的两焦点与短轴的一个端点的连线构成面积为
的两焦点与短轴的一个端点的连线构成面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,试问:在
两点,试问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为等边三角形,若存在,求直线
为等边三角形,若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在;直线
;(2)存在;直线![]() 的方程为
的方程为![]() .
.
【解析】
(1)由椭圆两焦点与短轴的一个端点的连线构成面积为![]() 的等腰直角三角形,可得
的等腰直角三角形,可得![]() 和椭圆标准方程.
和椭圆标准方程.
(2)由(1)可知椭圆方程![]() ,把直线
,把直线![]() 代入椭圆方程
代入椭圆方程![]() ,消
,消![]() 得
得![]() ,由韦达定理和弦长公式表示出
,由韦达定理和弦长公式表示出![]() ,再由韦达定理和
,再由韦达定理和![]() 点(由
点(由![]() 的垂直平分线方程中令x=0求得)到直线距离求得
的垂直平分线方程中令x=0求得)到直线距离求得![]() ,然后令
,然后令![]() ,解出
,解出![]() ,再检验判别式,写出直线的方程.
,再检验判别式,写出直线的方程.
(1)依题意得: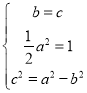 ,解得
,解得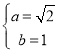
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
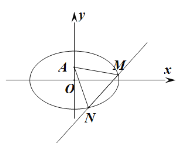
(2)假设在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 为等边三角形,设
为等边三角形,设![]() ,
,![]() ,
,
线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
把![]() 代入
代入![]()
并整理得,![]() ,
,
则![]() ,
,
解得![]() .
.
又![]() ,
,
所以![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
则直线![]() 的方程为
的方程为![]() ,
,
即![]() ,
,
令![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,又
,又![]() ,
,
即![]() 解得
解得![]() ,满足题意.
,满足题意.
所以在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() 为等边三角形,且直线
为等边三角形,且直线![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过其右焦点
,过其右焦点![]() 与长轴垂直的直线与椭圆在第一象限交于点
与长轴垂直的直线与椭圆在第一象限交于点![]() ,且
,且![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上的动点,且点
是椭圆上的动点,且点![]() 与点
与点![]() ,
,![]() 不重合,直线
不重合,直线![]() ,
,![]() 与直线
与直线![]() 分别交于点
分别交于点![]() ,
,![]() ,求证:以线段
,求证:以线段![]() 为直径的圆过定点.
为直径的圆过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间中两条直线![]() ,
,![]() 所成的角为50°,
所成的角为50°,![]() 为空间中给定的一个点,直线
为空间中给定的一个点,直线![]() 过点
过点![]() 且与直线
且与直线![]() ,
,![]() 所成的角都是
所成的角都是![]() ,则下列判断中正确的是( )
,则下列判断中正确的是( )
①当![]() 时,满足题意的直线
时,满足题意的直线![]() 不存在;②当
不存在;②当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且只有1条;③当
有且只有1条;③当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且只有2条;④当
有且只有2条;④当![]() 时,满足题意的直线
时,满足题意的直线![]() 有且只有3条.
有且只有3条.
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是圆O:x2+y2=16上的任意一点,m是过点D且与x轴垂直的直线,E是直线m与x轴的交点,点Q在直线m上,且满足2|EQ|![]() |ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
|ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程.
(2)已知点P(2,3),过F(2,0)的直线l交曲线C于A,B两点,交直线x=8于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
![]() ,若
,若![]() 是公差不为0的等差数列,且
是公差不为0的等差数列,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)记![]() ,若存在
,若存在![]() ,
,![]() (
(![]() ),使得
),使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程![]() 非一户一表用户电费采用“合表电价”收费标准:
非一户一表用户电费采用“合表电价”收费标准:![]() 元
元![]() 度
度![]() “一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档 | 第二档 | 第三档 | |
每户每月用电量 |
|
|
|
电价 |
|
|
|
例如:某用户11月用电410度,采用合表电价收费标准,应交电费![]() 元,若采用阶梯电价收费标准,应交电费
元,若采用阶梯电价收费标准,应交电费![]() 元.
元.
为调查阶梯电价是否能到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量![]() 单位:度
单位:度![]() 为:88、268、370、140、440、420、520、320、230、380.
为:88、268、370、140、440、420、520、320、230、380.

(1)在答题卡中完成频率分布表,并绘制频率分布直方图;

![]() 根据已有信息,试估计全市住户11月的平均用电量
根据已有信息,试估计全市住户11月的平均用电量![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 设某用户11月用电量为x度
设某用户11月用电量为x度![]() ,按照合表电价收费标准应交
,按照合表电价收费标准应交![]() 元,按照阶梯电价收费标准应交
元,按照阶梯电价收费标准应交![]() 元,请用x表示
元,请用x表示![]() 和
和![]() ,并求当
,并求当![]() 时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于
时,x的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于![]() 的用户带来实惠?
的用户带来实惠?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)当a=1 时,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在北宋年间(公元1084年)第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰,哈三中图书馆中正好有这十本书,但是书名中含有“算”字的书都已经借出,现在小张同学从剩余的书中任借两本阅读,那么他借到《数书九章》的概率为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com