【题目】若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（x+1）﹣f（x）=4x+1，且f（0）=3．
（1）求f（x）的解析式；
（2）若在区间[﹣1，1]上，不等式f（x）＞6x+m恒成立，求实数m的取值范围．
【答案】
（1）解：由f（0）=3得，c=3．∴f（x）=ax2+bx+3．
又f（x+1）﹣f（x）=4x+1，∴a（x+1）2+b（x+1）+3﹣（ax2+bx+3）=4x+1，
即2ax+a+b=4x+1，
∴ 
，∴ 
．∴f（x）=2x2﹣x+3
（2）解：f（x）＞6x+m等价于2x2﹣x+3＞6x+m，即2x2﹣7x+3＞m在[﹣1，1]上恒成立，
令g（x）=2x2﹣7x+3，则g（x）min=g（1）=﹣2，∴m＜﹣2
【解析】（1）利用f（0）=3求出c，利用f（x+1）﹣f（x）=4x+1求出a，b，即可求f（x）的解析式；（2）在区间[﹣1，1]上，不等式f（x）＞6x+m恒成立，转化为二次函数的闭区间上的最值，求解实数m的取值范围．
仁爱英语同步练习册系列答案
学习实践园地系列答案科目：高中数学 来源： 题型：
【题目】若f（x）是定义在R上的增函数，下列函数中
①y=[f（x）]2是增函数；
②y= 
是减函数；
③y=﹣f（x）是减函数；
④y=|f（x）|是增函数；
其中正确的结论是（ ）
A.③
B.②③
C.②④
D.①③
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合A={y|y=log2x，x≥4}，B={y|y=（ 
）x ， ﹣1≤x≤0}．
（1）求A∩B；
（2）若集合C={x|a≤x≤2a﹣1}，且C∪B=B，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛，甲对A，乙对B，丙对C各一盘，已知甲胜A，乙胜B，丙胜C的概率分别为0.6，0.5，0.5，假设各盘比赛结果相互独立．
（1）求红队至少两名队员获胜的概率；
（2）用ξ表示红队队员获胜的总盘数，求ξ的分布列和数学期望Eξ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=log4（4x+1）﹣ 
x．
（1）试判断函数f（x）的奇偶性并证明；
（2）设g（x）=log4（a2x﹣ 
a），若函数f（x）与g（x）的图象有且只有一个公共点，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近期“共享单车”在全国多个城市持续升温，某移动互联网机构通过对使用者的调查得出，现在市场上常见的八个品牌的“共享单车”的满意度指数如茎叶图所示：
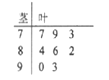
（Ⅰ）求出这组数据的平均数和中位数；
（Ⅱ）某用户从满意度指数超过80的品牌中随机选择两个品牌使用，求所选两个品牌的满意度指数均超过85的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
