
【题目】如图,在同一个平面内,向量 ![]() ,
, ![]() ,
, ![]() 的模分别为1,1,
的模分别为1,1, ![]() ,
, ![]() 与
与 ![]() 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, ![]() 与
与 ![]() 的夹角为45°.若
的夹角为45°.若 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 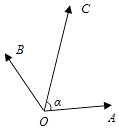
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,则λ+μ的最大值为( )
,则λ+μ的最大值为( )
A.3
B.2 ![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记“![]() ”为事件A,求事件A的概率;
”为事件A,求事件A的概率;
②在区间![]() 内任取2个实数
内任取2个实数![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上且周期为1的函数,在区间[0,1)上,f(x)= ![]() ,其中集合D={x|x=
,其中集合D={x|x= ![]() ,n∈N*},则方程f(x)﹣lgx=0的解的个数是 .
,n∈N*},则方程f(x)﹣lgx=0的解的个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com