【答案】
分析:(1)求函数f(x)的导数,由于导数中存在参数m,其取值范围的不同会造成函数的单调区间不同,极值的存在与否不同,故需要对参数m分类讨论,在每一类中求函数的极值;
(2)观察题设,要比较大小的几个数值的函数名不同,不易借助同一个函数的单调性来进行判断,本题采取了构造一个新函数的方法,借用新函数的单调性来比较两数的大小,对于函数名相同的两个数值大小的比较,直接作差即可.
解答:解:(1)∵当x>0时,f(x)=e
x-1在上单调递增,且f(x)=e
x-1>0
当x≤0时,f(x)=

x
3+mx
2,此时f′(x)=x
2+2mx=x(x+2m)
①当m=0时,f′(x)=x
2≥0,则f(x)=

x
3在(-∞,0】上单调递增且f(x)=

x
3≤0,又f(0)=0,可知函数f(x)在R上单调递增,故无极值.
②当m<0时同理,函数f(x)在R上单调递增,故无极值
③当m>0时,令f′(x)=x(x+2m)>0,得x>0或x<-2m.此时函数f(x)=

x
3+mx
2在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.
∴函数在f(x)x=-2m处取得极大值f(-2m)=
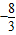
m
3+4m
3=

m
3>0;
又∵f(x)在(0,+∞)上单调递增,故函数f(x)在x=0处取得极小值f(0)=0.
综上可知:当m>0时,f(x)的极大值为

m
3,极小值为0;当m≤时,f(x)无极值
(2)当x>0时,设y=f(x)=e
x-1则x=ln(y+1)
∴f
-1(x)=ln(x+1)(x>0)
①比较f(q-p)与f
-1(q-p)的大小.
记g(x)=f(x)-f
-1(x)=e
x-ln(x+1)-1(x>0)
∵当x>0时,有g′(x)>g′(0)=0恒成立.
∴函数g(x)在(0,+∞)上单调递增,又因为g(x)在x=0处连续
∴当x>0时,有g(x)>g(0)=e
-ln(0+1)-1=0
当0<p<q时,有p-p>0,
∴g(q-p)=f(q-p)-f
-1(q-p)>0,即f(q-p)>f
-1(q-p)
②比较f
-1(q-p)与f
-1(q)-f
-1(p)的大小
∵f
-1(q-p)-[f
-1(q)-f
-1(p)]=ln(q-p+1)-ln(q+1)+ln(p+1)
∵0<p<q,∴
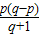
+1>1,
∴ln[
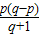
+1]>0
∴g(q-p)>f(q)-f
-1(p)
由①②可知,当0<p<q时,有f(q-p)>f
-1(q-p)>f
-1(q)-f
-1(p)
点评:本题考点是利用导数研究函数的极值,考查了函数极值存在的条件,利用导数研究函数的单调性,以及利用单调性比较大小,本题也涉及了对数与指数的运算,故本题辞让强,综合性强,解答时注意体会本题问题的转化技巧与方法.

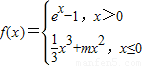 (m∈R,e是自然常数).
(m∈R,e是自然常数). x3+mx2,此时f′(x)=x2+2mx=x(x+2m)
x3+mx2,此时f′(x)=x2+2mx=x(x+2m) x3在(-∞,0】上单调递增且f(x)=
x3在(-∞,0】上单调递增且f(x)= x3≤0,又f(0)=0,可知函数f(x)在R上单调递增,故无极值.
x3≤0,又f(0)=0,可知函数f(x)在R上单调递增,故无极值. x3+mx2在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.
x3+mx2在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.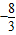 m3+4m3=
m3+4m3= m3>0;
m3>0; m3,极小值为0;当m≤时,f(x)无极值
m3,极小值为0;当m≤时,f(x)无极值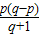 +1>1,
+1>1,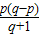 +1]>0
+1]>0

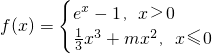 (m∈R,e是自然常数).
(m∈R,e是自然常数).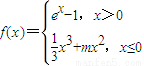 (m∈R,e是自然常数).
(m∈R,e是自然常数).