
【题目】汕头某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔腾6号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题:(1)引进该设备多少年后,收回成本并开始盈利?(2)引进该设备若干年后,有两种处理方案:第一种:年平均盈利达到最大值时,以26万元的价格卖出;第二种:盈利总额达到最大值时,以8万元的价格卖出.问哪种方案较为合算?并说明理由.
【答案】解:(1)设引进设备n年后开始盈利,盈利为y万元,
则y=50n-(12n+![]() ×4)-98=-2n2+40n-98,由y>0,得10-
×4)-98=-2n2+40n-98,由y>0,得10-![]() <n<10+
<n<10+![]() .
.
∵n∈N*,∴3≤n≤17,即3年后开始盈利.…………………6分
(2)方案一:年平均盈利为![]() ,
,![]() =-2n-
=-2n-![]() +40≤-2
+40≤-2![]() +40=12,
+40=12,
当且仅当2n=![]() ,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
方案二:盈利总额y=-2(n-10)2+102,n=10时,y取最大值102,
即经过10年盈利总额最大,
共计盈利102+8=110万元.
两种方案获利相等,但由于方案二时间长,所以采用方案一合算.…………12分
【解析】
试题(1)根据利润等于收入-成本,可求利润函数,令其大于0,可得结论;
(2)分别求出两种处理方案的利润,再进行比较,即可得到结论.
试题解析:(1)设引进设备n年后开始盈利,盈利为y万元,
则y=50n-(12n+![]() ×4)-98=-2n2+40n-98,
×4)-98=-2n2+40n-98,
由y>0,得10-![]() <n<10+
<n<10+![]() .
.
∵n∈N*,∴3≤n≤17,即3年后开始盈利.
(2)方案一:年平均盈利为![]() ,
,![]() =-2n-
=-2n-![]() +40≤-2
+40≤-2![]() +40=12,
+40=12,
当且仅当2n=![]() ,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
方案二:盈利总额y=-2(n-10)2+102,n=10时,y取最大值102,
即经过10年盈利总额最大, 共计盈利102+8=110万元.
两种方案获利相等,但由于方案二时间长,所以采用方案一合算.


科目:高中数学 来源: 题型:
【题目】执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )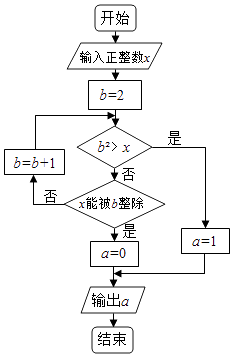
A.0,0
B.1,1
C.0,1
D.1,0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.
(Ⅰ)M为曲线C1上的动点,点P在线段OM上,且满足|OM||OP|=16,求点P的轨迹C2的直角坐标方程;
(Ⅱ)设点A的极坐标为(2, ![]() ),点B在曲线C2上,求△OAB面积的最大值.
),点B在曲线C2上,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是满足下列条件的函数
是满足下列条件的函数![]() 的全体:在定义域内存在实数
的全体:在定义域内存在实数![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)判断幂函数![]() 是否属于集合
是否属于集合![]() ?并说明理由;
?并说明理由;
(Ⅱ)设![]() ,
, ![]() ,
,
i)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
ii)若对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)为考察某种药物预防疾病的效果,进行动物试验,调查了105个样本,统计结果为:服药的共有55个样本,服药但患病的仍有10个样本,没有服药且未患病的有30个样本.
(1)根据所给样本数据完成2×2列联表中的数据;
(2)请问能有多大把握认为药物有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(Ⅰ)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(Ⅱ)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程是 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1,
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1, ![]() )
)
(1)求直线AB的直角坐标方程;
(2)在曲线C上求一点M,使点M到AB的距离最大,并求出些最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com