
分析 (1)由已知得x>-1,f′(x)=ln(x+1)+1,x∈(-1,$\frac{1}{e}$-1)时,f′(x)<0;当x∈($\frac{1}{e}-1$,+∞)时,f′(x)>0.由此求出x=$\frac{1}{e}$-1时,[f(x)]min=f($\frac{1}{e}-1$),由此能求出结果.
(2)令g(x)=(x+1)ln(x+1)-ax,对函数g(x)求导数:g′(x)=ln(x+1)+1-a令g′(x)=0,得x=ea-1-1,由此根据a≤1,a>1进行分类讨论,利用导数性质能求出a的取值范围.
解答 解:(1)∵f(x)=(x+1)ln(x+1),
∴x+1>0,解得x>-1,
f′(x)=ln(x+1)+1,
令f′(x)=0,得x+1=$\frac{1}{e}$,即x=$\frac{1}{e}-1$,
当x∈(-1,$\frac{1}{e}$-1)时,f′(x)<0;当x∈($\frac{1}{e}-1$,+∞)时,f′(x)>0.
∴x=$\frac{1}{e}$-1时,[f(x)]min=f($\frac{1}{e}-1$)=$\frac{1}{e}ln(\frac{1}{e})$=-$\frac{1}{e}$.
(2)令g(x)=(x+1)ln(x+1)-ax,
对函数g(x)求导数:g′(x)=ln(x+1)+1-a
令g′(x)=0,解得x=ea-1-1,
(i)当a≤1时,对所有x>0,g′(x)>0,所以g(x)在[0,+∞)上是增函数,
又g(0)=0,所以对x≥0,都有g(x)≥g(0),
即当a≤1时,对于所有x≥0,都有f(x)≥ax.
(ii)当a>1时,对于0<x<ea-1-1,g′(x)<0,所以g(x)在(0,ea-1-1)是减函数,
又g(0)=0,所以对0<x<ea-1-1,都有g(x)<g(0),
即当a>1时,不是对所有的x≥0,都有f(x)≥ax成立.
综上,a的取值范围是(-∞,1].
点评 本题考查函数的最小值的求法,考查实数的取值范围的求法,考查导数的性质的应用,考查推理论证能力、运算求解能力,考查转化化归思想、分类讨论思想,是中档题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
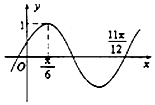 已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.
已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
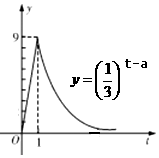 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com