
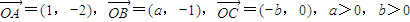 ,O为坐标原点,若A、B、C三点共线,则
,O为坐标原点,若A、B、C三点共线,则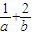 的最小值是( )
的最小值是( )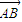 和
和 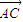 的坐标,再根据两个向量共线的性质得到2a+b=1,然后结合所求的式子的结构特征利用基本不等式求出其最小值.
的坐标,再根据两个向量共线的性质得到2a+b=1,然后结合所求的式子的结构特征利用基本不等式求出其最小值.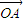 =(1,-2),
=(1,-2),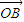 =(a,-1),
=(a,-1),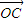 =(-b,0),
=(-b,0),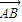 =
=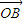 -
-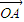 =(a-1,1),
=(a-1,1),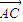 =
= -
-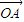 =(-b-1,2).
=(-b-1,2).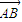 ∥
∥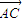 ,从而(a-1 )×2-1×(-b-1)=0,
,从而(a-1 )×2-1×(-b-1)=0, +
+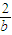 =(
=( 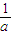 +
+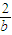 )•(2a+b)=4+(
)•(2a+b)=4+( 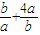 )≥4+4=8
)≥4+4=8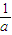 +
+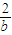 的最小值是8.
的最小值是8.

科目:高中数学 来源:2012-2013学年福建省泉州市安溪八中高三(上)12月月考数学试卷(理科)(解析版) 题型:选择题
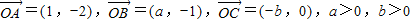 ,O为坐标原点,若A、B、C三点共线,则
,O为坐标原点,若A、B、C三点共线,则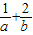 的最小值是( )
的最小值是( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市安溪八中高三(上)12月月考数学试卷(理科)(解析版) 题型:选择题
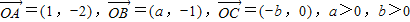 ,O为坐标原点,若A、B、C三点共线,则
,O为坐标原点,若A、B、C三点共线,则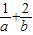 的最小值是( )
的最小值是( )查看答案和解析>>
科目:高中数学 来源:2007-2008学年重庆八中高三(下)第一次月考数学试卷(文科)(解析版) 题型:选择题
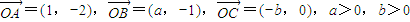 ,O为坐标原点,若A、B、C三点共线,则
,O为坐标原点,若A、B、C三点共线,则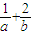 的最小值是( )
的最小值是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com