
����Ŀ��2017 ��ʡ��ij��ҵ��λ������ṫ���гҹ�����Ա��Ϊ��֤��ƽ��������������Ҫ�μӱ��Ժ����������֣���Ҫ����Գɼ�������ڻ����![]() �ֵIJ����ʸ�μ����ԣ�
�ֵIJ����ʸ�μ����ԣ� ![]() �����£�����
�����£�����![]() �֣�����̭������
�֣�����̭������![]() �������߲μӱ��ԣ��μӱ��Եijɼ�������
�������߲μӱ��ԣ��μӱ��Եijɼ�������![]() �ֶΣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�����𣩣�����֪���μ����Ե�����Ϊ
�ֶΣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�����𣩣�����֪���μ����Ե�����Ϊ![]() ���ұ��Գɼ���
���ұ��Գɼ���![]() ������Ϊ
������Ϊ![]() .
.

��1������Ƶ�ʷֲ�ֱ��ͼ�����㾺���߲μӱ��Ե�ƽ���ɼ���
��2���������Թ�����ÿ�������![]() ��ѡ�����Ļ��ᣬ�ۼƴ��
��ѡ�����Ļ��ᣬ�ۼƴ��![]() �����
�����![]() ��, ���
��, ���![]() ���߷��ɲμӸ�������֪�����״��ÿһ������ĸ��ʶ���ͬ�������֮��û��Ӱ�죬�����������δ����д��һ�εĸ���Ϊ
���߷��ɲμӸ�������֪�����״��ÿһ������ĸ��ʶ���ͬ�������֮��û��Ӱ�죬�����������δ����д��һ�εĸ���Ϊ![]() ���������״������
���������״������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
���𰸡���1��78.48����2��������.
�������������������1������Ƶ�ʷֲ�ֱ��ͼ��С�����������ʾ��ӦƵ�ʵĺ��壬ÿ��С���εľ�ֵ����Ƶ����ͼ��ɣ�
��2����������ÿ�����Եĸ���Ϊ![]() ����
����![]() �������״������
�������״������![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ����������ʼ���.
����������ʼ���.
���������
(1)�辺Ƹ�߳ɼ�������![]() �������ֱ�Ϊ
�������ֱ�Ϊ![]() ����
����![]() �����
�����![]() .
.![]() �����
�����![]() .
.![]() ,
,
���![]() ����Ƹ�߲μӱ��Ե�ƽ���ɼ�Ϊ
����Ƹ�߲μӱ��Ե�ƽ���ɼ�Ϊ
![]() .
.
(2)��������ÿ�����Եĸ���Ϊ![]() ����
����![]() �������״������
�������״������![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ����
����![]() ��
��
![]() .
. ![]() �ķֲ������±���
�ķֲ������±���
|
|
|
|
|
|
|
|
![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}��ǰn���Sn����Sn=2an+n��
������֤������{an��1}�ǵȱ����У�
����bn=![]() ��������{bn}��ǰn��ͣ�
��������{bn}��ǰn��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD��A1B1C1D1��8������������ȡ4����ͬ�Ķ��㣬��4����������ǣ�
1�����ε�4�����㣻
2��ÿ���涼�ǵȱ������ε��������4�����㣻
3��ÿ���涼��ֱ�������ε��������4�����㣻
4�����������ǵ���ֱ�������Σ���һ�����ǵȱ������ε��������4�����㣮
������ȷ���۵ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
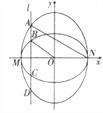
����Ŀ����ͼ����֪��Բ![]() ��������ԭ��
��������ԭ��![]() ���������Ҷ˵�
���������Ҷ˵�![]() ��
��![]() ��
��![]() ���ϣ���Բ
���ϣ���Բ![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ����
����![]() ��
��![]() �������ʶ�Ϊ
�������ʶ�Ϊ![]() ��ֱ��
��ֱ��![]() ,
, ![]() ��
��![]() �������㣬��
�������㣬��![]() �������㣬���ĵ�������Ӵ�С����Ϊ
�������㣬���ĵ�������Ӵ�С����Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .
.
��1����![]() ����
����![]() ��
��![]() �ı�ֵ��
�ı�ֵ��
��2��������ֱ��![]() ,ʹ��
,ʹ��![]() ��������Բ������
��������Բ������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A(3,5)��B(��1,3)��C(��3,1)Ϊ��ABC���������㣬O��M��N�ֱ�Ϊ��AB��BC��CA���е㣬���OMN�����Բ�ķ��̣��������Բ��Բ�ĺͰ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ��
��![]() �������ҽ���ֱ�Ϊ
�������ҽ���ֱ�Ϊ![]() ��
�� ![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ����Բ
����Բ![]() �ϣ�
�ϣ� ![]() ��
�� ![]() ����
����![]() ���������ֱ��ֱ��
���������ֱ��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
�� ![]() ���㣮
���㣮
��������Բ![]() �ķ��̣�
�ķ��̣�
������![]() ��
�� ![]() ���е�Ϊ
���е�Ϊ![]() �����߶�
�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ���ʵ��
�������ڣ���ʵ��![]() ��ȡֵ��Χ���������ڣ�˵�����ɣ�
��ȡֵ��Χ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��ǰ
��ǰ![]() ��ͼ�Ϊ
��ͼ�Ϊ![]() ��
�� ![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϣ�����
�ϣ�����![]() .
.
��1��������![]() �ǵȱ����У���ʵ��
�ǵȱ����У���ʵ��![]() ��ֵ��
��ֵ��
��2����������Ϊ0������![]() �У���������
����������![]() ������
������![]() �ĸ�����Ϊ�������
�ĸ�����Ϊ�������![]() �ġ��������������
�ġ��������������![]() ��
��![]() �����ڣ�1���������£�������
�����ڣ�1���������£�������![]() �ġ����������.
�ġ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Գ�.
�Գ�.
��1������ʽ![]() ������
������![]() ���������ʵ��
���������ʵ��![]() �����ֵ��
�����ֵ��
��2����![]() ��
��![]() �ڵ�ʵ��Ϊ
�ڵ�ʵ��Ϊ![]() ��
�� 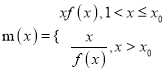 ����������
����������![]() �ϴ���
�ϴ���![]() ��֤����
��֤���� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ƕ�����D�ϵĺ���������������[m��n]D����ʵ��k��ʹ����f��x����[m��n]�ϵ�ֵ��ǡΪ[km��kn]����ƺ���f��x����k�ͺ�������������˵����
��f��x��=3�� ![]() ��������k�ͺ�����
��������k�ͺ�����
��������f��x��= ![]() ��a��0����1�ͺ�������n��m�����ֵΪ
��a��0����1�ͺ�������n��m�����ֵΪ ![]() ��
��
��������f��x��=�� ![]() x2+x��3�ͺ�������m=��4��n=0��
x2+x��3�ͺ�������m=��4��n=0��
������ȷ˵������Ϊ�� ��
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com