
【题目】选修4-4:坐标系与参数方程,在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为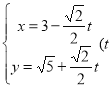 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极轴,以
为极轴,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某市为增强市民的环境保护意识, 面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取![]() 名按年龄分组: 第
名按年龄分组: 第![]() 组
组![]() ,第2 组
,第2 组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,
,得到的频率分布直方图如图所示,
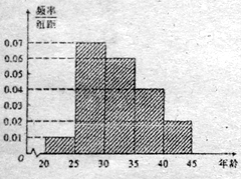
(1)若从第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参与广场的宣传活动, 应从第
名志愿者参与广场的宣传活动, 应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(2)在(1)的条件下, 该县决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验, 求第
名志愿者介绍宣传经验, 求第![]() 组至少有—名志愿者被抽中的概率.
组至少有—名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点

(1)求四棱锥P-ABCD的体积;
(2)证明:BD⊥AE。
(3)求二面角P-BD-C的正切值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015;已知函数f(x)=a2sin(ωx+φ)(ω>0,|φ|<![]() )的最小正周期是a1,且函数
)的最小正周期是a1,且函数![]() 的图象关于直线x=
的图象关于直线x=![]() 对称。
对称。

(Ⅰ)求函数![]() 表达式;
表达式;
(Ⅱ)已知△ABC中三边a,b,c对应角A,B,C,a=4,b=4![]() ,∠A=30°,求
,∠A=30°,求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十一国庆节期间,某商场举行购物抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为![]() ,中奖可以获得3分;方案乙的中奖率为
,中奖可以获得3分;方案乙的中奖率为![]() ,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为![]() ,求
,求![]() 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,分别求两种方案下小明、小红累计得分的分布列,并指出为了累计得分较大,两种方案下他们选择何种方案较好,并给出理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com