
| A、“f(O)=O”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、“向量a,b,c,若a•b=a•c,则b=c”是真命题 | ||||||||
C、函数f(x)=
| ||||||||
D、“若α=
|
| 1 |
| x |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| 1 |
| e |
| 1 |
| 3e |
| 1 |
| 3 |
| e |
| 3 |
| 1 |
| x |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| 1 |
| e |
| 1 |
| 3e |
| 1 |
| 3 |
| e |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
| x |
| 2+x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
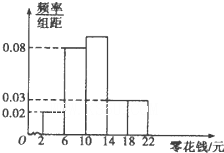 一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有
一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 3a2 |
| y2 |
| b2 |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+1 |
| an |
| an+1 |
| an |
| 1 |
| 3 |
| 1-(3c)n |
| 1-3c |
| 2xn-1+3 |
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、g(a)<0<f(b) |
| B、f(b)<0<g(a) |
| C、0<g(a)<f(b) |
| D、f(b)<g(a)<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com