
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
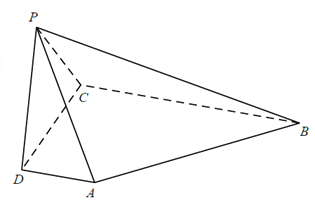
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为棱
为棱![]() 上的点.
上的点.

![]() 证明:
证明:![]() ;
;
![]() 证明:
证明:![]() ;
;
![]() 是否存在一点
是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,说明点
?若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,已知平面
中,已知平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在棱
在棱![]() 上且满足
上且满足![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网经济逐步被人们接受,网上购物的人群越来越多,网银交易额也逐年增加,某地连续五年的网银交易额统计表,如表所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网银交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,工作人员将上表的数据进行了处理,![]() ,
,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)用所求回归方程预测2020年该地网银交易额.
(附:在线性回归方程![]() 中,
中,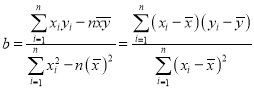 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com