练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某工厂拟建一座平面图为矩形，面积为，高度一定的三段污水处理池（如图），由于受地形限制，其长、宽都不超过，如果池的外壁的建造费单价为元，池中两道隔壁墙（与宽边平行）的建造费单价为元，池底的建造费单价为元.设水池的长为，总造价为.

    （1）求的表达式；

    （2）水池的长与宽各是多少时，总造价最低，并求出这个最低造价.

    【答案】（1）；（2）水池长为，宽为，最低造价为元.

    【解析】

    （1）水池长为，可得其宽为，由其长、宽都不超过可求得的取值范围，根据题意可得出函数的表达式；

    （2）利用基本不等式可求得函数的最小值，利用等号成立的条件可求得水池的长与宽，进而得解.

    （1）水池的长为，则宽为，由题意可得，解得，

    ，

    ；

    （2），

    当且仅当，即时取等号，此时，.

    因此，当水池长为，宽为，其总造价最低，最低造价为元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】记函数的定义域为D. 如果存在实数、使得对任意满

    足且的x恒成立，则称为函数.

    （1）设函数，试判断是否为函数，并说明理由；

    （2）设函数，其中常数，证明： 是函数；

    （3）若是定义在上的函数，且函数的图象关于直线（m为常数）对称，试判断是否为周期函数？并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（，）．

    （1）若在上单调递减，求的取值范围；

    （2）当时，判断关于的方程的解的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】边长为的等边三角形内任一点到三边距离之和为定值，这个定值等于；将这个结论推广到空间是：棱长为的正四面体内任一点到各面距离之和等于________________.（具体数值）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm），获得身高数据的茎叶图如图7.

    （1）根据茎叶图判断哪个班的平均身高较高；

    （2）计算甲班的样本方差；

    （3）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数,.

    （1）若，求的单调区间；

    （2）求函数在上的最值；

    （3）当时，若函数恰有两个不同的零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

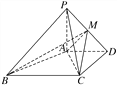
    【题目】如图，在四棱锥PABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD＝CD＝2，BC＝4，PA＝2.

    (1)求证：AB⊥PC；

    (2)在线段PD上，是否存在一点M，使得二面角MACD的大小为45°，如果存在，求BM与平面MAC所成角的正弦值，如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在坐标原点，一个焦点为的椭圆被直线截得的弦的中点的横坐标为.

    （1）求此椭圆的方程；

    （2）设直线与椭圆交于两点，且以为对角线的菱形的一个顶点为，求面积的最大值及此时直线的方程.

    查看答案和解析>>

    同步练习册答案