
| A. | $\frac{n-1}{n}$ | B. | $\frac{2n-2}{n}$ | C. | $\frac{1-n}{n}$ | D. | $\frac{2-2n}{n}$ |
分析 根据通项公式求得展开式中x-4的系数为an =${C}_{n}^{2}$=$\frac{n(n-1)}{2}$,可得$\frac{1}{{a}_{n}}$=2($\frac{1}{n-1}$-$\frac{1}{n}$),从而求得要求式子的值.
解答 解:(1-$\frac{1}{{x}^{2}}$)n(n∈N*,n>1)的展开式的通项公式为 Tr+1=${C}_{n}^{r}$•(-1)r•x-2r,
故展开式中x-4的系数为an =${C}_{n}^{2}$=$\frac{n(n-1)}{2}$,∴$\frac{1}{{a}_{n}}$=2($\frac{1}{n-1}$-$\frac{1}{n}$),
∴$\frac{1}{{a}_{2}}+\frac{1}{{a}_{3}}+…+\frac{1}{{a}_{n}}$=2[(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n-1}$-$\frac{1}{n}$)]=2(1-$\frac{1}{n}$)=$\frac{2n-2}{n}$,
故选:B.
点评 本题主要考查二项式定理的应用,求展开式中某项的系数,用裂项法进行求和,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -2<t<-$\frac{4}{3}$ | B. | -2<t≤-$\frac{4}{3}$ | C. | -2≤t≤-$\frac{4}{3}$ | D. | -2≤t<-$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
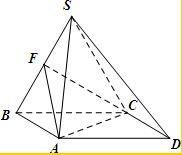 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com