
【题目】已知公差不为零的等差数列{an}的前n项和为Sn,S3=15,a1,a4,a13成等比数列.
(1)求数列{an}的通项公式;
(2)求数列![]() 的前n项和Tn大于2020的最小自然数n.
的前n项和Tn大于2020的最小自然数n.
【答案】(1)an=2n+1;(2)10.
【解析】
(1)设等差数列{an}的公差为d(d≠0),由题设条件列出d的方程,解出d,a1,求出通项公式;
(2)由(1)求得a![]() ,再使用分组求和求出Tn,研究其单调性,求出满足Tn大于2020的最小自然数n.
,再使用分组求和求出Tn,研究其单调性,求出满足Tn大于2020的最小自然数n.
(1)设等差数列{an}的公差为d(d≠0),则S3=3a1![]() 15,
15,
∴a1+d=5,a4=5+2d,a13=5+11d,
∵a1,a4,a13成等比数列,
∴(5+2d)2=(5![]() d)(5+11d),解得d=0(舍去)或d=2,
d)(5+11d),解得d=0(舍去)或d=2,
故a1=5![]() d=3.
d=3.
所以an=3+(n![]() 1)×2=2n+1.
1)×2=2n+1.
(2)根据(1)知a![]() 2(2n
2(2n![]() n)+1=2n+1
n)+1=2n+1![]() (2n
(2n![]() 1),
1),
∴Tn=(22+23+…+2n+1)![]() [1+3+…+(2n
[1+3+…+(2n![]() 1)]
1)]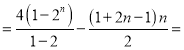 2n+2
2n+2![]() n2
n2![]() 4.
4.
∵2n![]() n>0,
n>0,
∴a![]() 2(2n
2(2n![]() n)+1>0,
n)+1>0,
∴Tn单调递增,
又∵T9<2020,T10>2020,
所以Tn大于2020的最小自然数n为10.
【点晴】
本题主要考查等差数列基本量的运算,数列的分组求和,数列的单调性,属于中档题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() ).下面表格所确定的点
).下面表格所确定的点![]() 中,恰有三个点在椭圆
中,恰有三个点在椭圆![]() 上.
上.
|
|
| 1 |
|
|
| 0 |
|
|
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为坐标原点,点
为坐标原点,点![]() ,
,![]() 分别为
分别为![]() 的上下顶点,直线
的上下顶点,直线![]() 经过
经过![]() 的右顶点
的右顶点![]() ,且与
,且与![]() 的另一个公共点为
的另一个公共点为![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() 与
与![]() 轴的交点
轴的交点![]() 异于
异于![]() ,
,![]() ,证明
,证明![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差不为0的等差数列,
是公差不为0的等差数列,![]() ,数列
,数列![]() 是等比数列,且
是等比数列,且![]() ,
,![]() ,
,![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设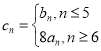 ,求
,求![]() 的前n项和
的前n项和![]() ;
;
(3)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程:
的参数方程: (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上一点
上一点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,中点为
两点,中点为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019新型冠状病毒感染的肺炎的传播有飞沫、气溶胶、接触等途径,为了有效抗击疫情,隔离性防护是一项具体有效措施.某市为有效防护疫情,宣传居民尽可能不外出,鼓励居民的生活必需品可在网上下单,商品由快递业务公司统一配送(配送费由政府补贴).快递业务主要由甲公司与乙公司两家快递公司承接:“快递员”的工资是“底薪+送件提成”.这两家公司对“快递员”的日工资方案为:甲公司规定快递员每天底薪为70元,每送件一次提成1元;乙公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成5元,假设同一公司的快递员每天送件数相同,现从这两家公司往年忙季各随机抽取一名快递员并调取其100天的送件数,得到如下条形图:

(1)求乙公司的快递员一日工资y(单位:元)与送件数n的函数关系;
(2)若将频率视为概率,回答下列问题:
①记甲公司的“快递员”日工资为X(单位:元).求X的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com