
【题目】某船由甲地逆水行驶到乙地,甲、乙两地相距s(km),水的流速为常量a(![]() ),船在静水中的最大速度为b(
),船在静水中的最大速度为b(![]() )(
)(![]() ),已知船每小时的燃料费用(以元为单位)与船在静水中的速度的平方成正比,比例系数为k,则船在静水中的航行速度为多少时,其全程的燃料费用最省?
),已知船每小时的燃料费用(以元为单位)与船在静水中的速度的平方成正比,比例系数为k,则船在静水中的航行速度为多少时,其全程的燃料费用最省?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到频数分布表和频率分布直方图如下.
组号 | 分组 | 频数 |
1 | [0,2) | 6 |
2 | [2,4) | 8 |
3 | [4,6) | 17 |
4 | [6,8) | 22 |
5 | [8,10) | 25 |
6 | [10,12) | 12 |
7 | [12,14) | 6 |
8 | [14,16) | 2 |
9 | [16,18) | 2 |
合计 | 100 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率分布直方图中的a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间中![]() 个平面,其中任意三个平面无公垂面.那么,下述四个结论
个平面,其中任意三个平面无公垂面.那么,下述四个结论
1没有任何两个平面互相平行;
2没有任何三个平面相交于一条直线;
3平面间的任意两条交线都不平行;
4平面间的每一条交线均与![]() 个平面相交.
个平面相交.
其中,正确的各数为( ).
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2名女生和4名男生外出参加比赛活动.
(1)他们排成一列照相时,若2名女生必须在一起,有多少种排列方法?
(2)他们排成一列照相时,若2名女生不相邻,有多少种排列方法?
(3)从这6名学生中挑选3人担任裁判,至少要有1名女生,则有多少种选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示将同心圆环均匀分成n(![]() )格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
)格.在内环中固定数字1~n.问能否将数字1~n填入外环格内,使得外环旋转任意格后有且仅有一个格中内外环的数字相同?
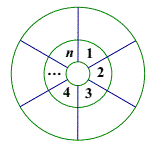
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两校各有3名教师报名支教,期中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一商家诚邀甲、乙两名围棋高手进行一场网络国棋比赛,每比赛一局商家要向每名棋手支付2000元对局费,同时商家每局从转让网络转播权及广告宣传中获利12100元,从两名棋手以往比赛中得知,甲每局获胜的概率为![]() ,乙每局获胜的概率为
,乙每局获胜的概率为![]() ,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
,两名棋手约定:最多下五局,先连胜两局者获胜,比赛结束,比赛结束后,商家为获胜者颁发5000元的奖金,若没有决出获胜者则各颁发2500元.
(1)求下完五局且甲获胜的概率是多少;
(2)求商家从这场网络棋赛中获得的收益的数学期望是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com