
【题目】执行如图程序框图,如果输入的a=4,b=6,那么输出的n=( )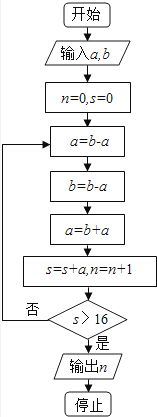
A.3
B.4
C.5
D.6
【答案】B
【解析】解:模拟执行程序,可得
a=4,b=6,n=0,s=0
执行循环体,a=2,b=4,a=6,s=6,n=1
不满足条件s>16,执行循环体,a=﹣2,b=6,a=4,s=10,n=2
不满足条件s>16,执行循环体,a=2,b=4,a=6,s=16,n=3
不满足条件s>16,执行循环体,a=﹣2,b=6,a=4,s=20,n=4
满足条件s>16,退出循环,输出n的值为4.
故选:B.
模拟执行程序,根据赋值语句的功能依次写出每次循环得到的a,b,s,n的值,当s=20时满足条件s>16,退出循环,输出n的值为4.本题主要考查了循环结构的程序框图的应用,正确依次写出每次循环得到的a,b,s的值是解题的关键,属于基础题.


科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)当![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅱ)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示 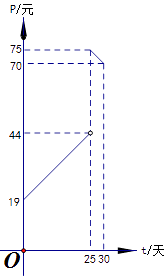
(1)写出销售价格P(元)和时间t(天)的函数解析式;
(2)若日销售量Q(件)与时间t(天)的函数关系是Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)问该产品投放市场第几天时,日销售金额最高?最高值为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知标有1~20号的小球20个,若我们的目的是估计总体号码的平均值,即20个小球号码的平均值.试验者从中抽取4个小球,以这4个小球号码的平均值估计总体号码的平均值,按下面方法抽样(按小号到大号排序):
(1)以编号2为起点,系统抽样抽取4个球,则这4个球的编号的平均值为____.
(2)以编号3为起点,系统抽样抽取4个球,则这4个球的编号的平均值为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于利用斜二侧法得到的直观图有下列结论:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形,以上结论正确的是( )
A. ①② B. ① C. ③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com