
已知数列 是一个等差数列,
是一个等差数列,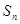 是其前
是其前 项和,且
项和,且 ,
, .
.
(1)求 的通项
的通项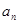 ;
;
(2)求数列 的前10项的和
的前10项的和
科目:高中数学 来源: 题型:解答题
某公司经销一种数码产品,第一年可获利200万元,从第二年起,由于市场竞争等方面的原因,其利润每年比上一年减少20万元,按照这一规律,如果公司不开发新产品,也不调整经营策略,从哪一年起,该公司经销这一产品将亏损?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com