设x=-1是f(x)=(x2+ax+b)e2-x(x∈R)的一个极值点,
(1)求a与b的关系式(用a表示b)并求f(x)的单调区间
(2)是否存在实数m,使得对任意a∈(-2,-1)及λ1λ2∈[-2,1]总有|f(λ1)-f(λ2)|<[(m+2)a+1]e3恒成立,若存在求出m的范围.若不存在,说明理由.
【答案】
分析:(1)首要的是求出函数的导数,利用已知函数在x=-1处取得极值,可以建立参数a,b的关系,从而利用a表达出b,另外x=-1是极值点可得a≠-4,因此要注意对a进行讨论:a<-4和a>-4,从而求出函数的单调区间;
(2)根据函数的单调性求出函数f(x)的值域,设存在实数m满足题设,依题意有:[(m+2)a+1]e
3>e
4-(a-2)e
3恒成立,从而(m+3)a-e-1>0恒成立,看成关于a的一次函数在[-2,1]上恒成立,建立关系式,解之即可.
解答:解:(1)f'(x)=-[x
2+(a-2)x+b-a]e
2-x由f'(-1)=0得b=2a-3…(2分)∴f(x)=(x
2+ax+2a-3)e
2-x
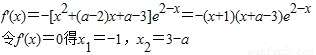
由于x=-1是f(x)的极值点,故x
1≠x
2,即a≠4
①当a<4时,x
2>x
1,故[-1,3-a]为f(x)的单调增区间;(-∞,-1]、[3-a,+∞)为f(x)
的单调减区间.…(4分)
②当a>4时,x
2<x
1,故[[3-a,-1]为f(x)的单调增区间;(-∞,3-a]、[-1,+∞)为f(x)的单调减区间…(6分)
(2)由-2<a<-1得4<3-a<5,从而知f(x)在[-2,-1]单调递减,在[-1,1]上单调递增,
f(x)的值域为[f(-1),max{f(-2),f(1)}]=[(a-2)e
3,e
4]…(8分)
假设存在实数m满足题设,依题意有:[(m+2)a+1]e
3>e
4-(a-2)e
3恒成立,
即(m+3)a-e-1>0恒成立,…(12分)
令g(a)=(m+3)a-e-1,
则有
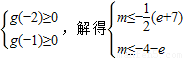
,即m≤-4-e
故存在实数m∈(-∞,-4-e]满足题设.…(14分)
点评:本题主要考查了利用导数研究函数的单调性,以及函数恒成立问题和极值等有关问题,是一道综合题,属于中档题

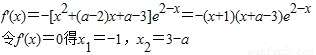
 ,即m≤-4-e
,即m≤-4-e

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案