
△ABC中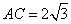 , B是椭圆
, B是椭圆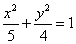 在x轴上方的顶点,
在x轴上方的顶点,  是双曲线
是双曲线 位于x轴下方的准线, 当AC在直线
位于x轴下方的准线, 当AC在直线 上运动时.
上运动时.
(1)求△ABC外接圆的圆心P的轨迹E的方程;
(2)过定点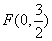 作互相垂直的直线
作互相垂直的直线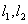 , 分别交轨迹E于M、N和R、Q, 求四边形MRNQ面积的最小值.
, 分别交轨迹E于M、N和R、Q, 求四边形MRNQ面积的最小值.
解:(1)由椭圆方程 及双曲线方程
及双曲线方程 可得点
可得点 直线
直线 方程是
方程是
 且
且 在直线
在直线 上运动。
上运动。
可设
则 的垂直平分线方程为
的垂直平分线方程为 ①
①
 的垂直平分线方程为
的垂直平分线方程为 ②
②
 P是△ABC的外接圆圆心,
P是△ABC的外接圆圆心, 点P的坐标
点P的坐标 满足方程①和②
满足方程①和②
由①和②联立消去 得
得
故圆心P的轨迹E的方程为 --------------------------------------------------------(6分)
--------------------------------------------------------(6分)
(2)由图可知,直线 和
和 的斜率存在且不为零,设
的斜率存在且不为零,设 的方程为
的方程为 ,
,
 ,
, 的方程为
的方程为
由
得  ------------------------------(8分)
------------------------------(8分)
 △=
△= 直线
直线 与轨迹E交于两点。
与轨迹E交于两点。
设 ,则
,则 。
。

同理可得:
 四边形MRNQ的面积
四边形MRNQ的面积
 ------------(12分)
------------(12分)
当且仅当 ,即
,即 时,等号成立。
时,等号成立。
故四边形MNRQ的面积的最小值为72。----------------------------------------------------(13分)


科目:高中数学 来源: 题型:
| 3 |
| x2 |
| 5 |
| y2 |
| 4 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
在△ABC中![]() ,B是椭圆
,B是椭圆![]() 在x轴上方的顶点,
在x轴上方的顶点,![]() 是双曲线
是双曲线![]() 位于x轴下方的准线,当AC在直线
位于x轴下方的准线,当AC在直线![]() 上运动时。
上运动时。
(1)求△ABC外接圆的圆心P的轨迹E的方程;
(2)过定点![]() 作互相垂直的直线
作互相垂直的直线![]() ,分别交轨迹E于M、N和R、Q,求四边形MRNQ面积的最小值。
,分别交轨迹E于M、N和R、Q,求四边形MRNQ面积的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com