
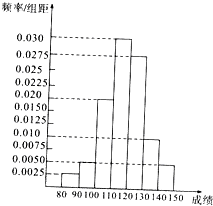
 某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试,为了解数学学科的成绩情况,现从中随机抽取若干名学生在这次测试中的数学成绩作为样本,(其中甲学校抽取了30人),制成如下频率分布表并得到相应的频率分布直方图:
某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试,为了解数学学科的成绩情况,现从中随机抽取若干名学生在这次测试中的数学成绩作为样本,(其中甲学校抽取了30人),制成如下频率分布表并得到相应的频率分布直方图:| 分组 | 频数 | 频率 |
| [80,90) | 0.025 | |
| [90,100) | 6 | |
| [100,110) | ||
| [110,120) | ||
| [120,130) | ||
| [130,140) | 12 | |
| [140,150) | 0.05 | |
| 合计 |
分析 (1)由已知条件,利用频率分布直方图,能求出频率分布表.
(2)由已知得该次统计中抽取样本的合理方法是分层抽样,利用分层抽样的性质能求出设甲学校共有多少人参加了调研测试.
(3)样本在[80,100)的个体共有9个个体,其中有有3个个体落在[80,90)中,6个个体落在[90,100)中,由此利用等可能事件概率计算公式能求出至少有一个个体落在[90,100)的概率.
解答 解:(1)由已知条件,利用频率分布直方图,得频率分布表为:
| 分组 | 频数 | 频率 |
| [80,90) | 3 | 0.025 |
| [90,100) | 6 | 0.050 |
| [100,110) | 24 | 0.2 |
| [110,120) | 36 | 0.3 |
| [120,130) | 33 | 0.275 |
| [130,140) | 12 | 0.1 |
| [140,150) | 6 | 0.05 |
| 合计 | 120 | 1 |
点评 本题考查频率分布直方图的应用,考查分层抽样及性质的应用,考查概率的求法,是基础题,解题时要注意等可能事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,5) | C. | (2,5) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x | B. | y2=6x | C. | y2=8x | D. | y2=9x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 135° | C. | 45° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com