
【题目】定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)﹣g(x)极值点的情况是( ) 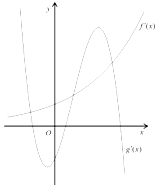
A.只有三个极大值点,无极小值点
B.有两个极大值点,一个极小值点
C.有一个极大值点,两个极小值点
D.无极大值点,只有三个极小值点
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】某电力部门需在A、B两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离.现测量人员在相距 ![]() km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的
km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的 ![]() 倍,问施工单位应该准备多长的电线?
倍,问施工单位应该准备多长的电线? 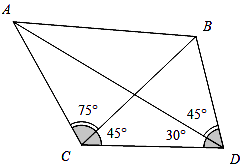
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若x∈D,y∈D,使得f(y)=﹣f(x)成立,则称函数f(x)为“美丽函数”.下列所给出的五个函数: ①y=x2;②y= ![]() ;③f(x)=ln(2x+3);④y=2x+3;⑤y=2sin x﹣1.
;③f(x)=ln(2x+3);④y=2x+3;⑤y=2sin x﹣1.
其中是“美丽函数”的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型 | 木地板A | 木地板B | 木地板C |
环保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3﹣3(a+1)x2+6ax+8,其中a∈R.已知f(x)在x=3处取得极值.
(1)求f(x)的解析式;
(2)求f(x)在点A(1,16)处的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如表数据:
单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为 ![]() =﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
=﹣4x+a.若在这些样本点中任取一点,则它在回归直线左下方的概率为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
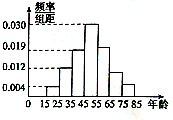
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com