
【题目】设Sn为数列{an}的前n项和,已知![]() ,对任意n∈N*,都有2Sn=(n+1)an.
,对任意n∈N*,都有2Sn=(n+1)an.
(1)求数列{an}的通项公式;
(2)若数列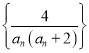 的前项和为Tn,求Tn的取值范围.
的前项和为Tn,求Tn的取值范围.
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=mxα的图象经过点A(2,2).
(1)试比较2ln f(3)与3ln f(2)的大小;
(2)定义在R上的函数g(x)满足g(-x)=g(x), g(4+x)=g(4-x),且当x∈[0,4]时,
 . 若关于x的不等式g 2(x)+ng(x)>0在[-200,200]上有且只有151个整数解,求实数n的取值范围。
. 若关于x的不等式g 2(x)+ng(x)>0在[-200,200]上有且只有151个整数解,求实数n的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,AB⊥BC,BA=BC![]() ,BD是边AC上的高,沿BD将△ABC折起,当三棱锥A﹣BCD的体积最大时,该三棱锥外接球表面积为( )
,BD是边AC上的高,沿BD将△ABC折起,当三棱锥A﹣BCD的体积最大时,该三棱锥外接球表面积为( )
A. 12πB. 24πC. 36πD. 48π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)如表所示是某市最近5年个人年平均收入表节选.求y关于x的回归直线方程,并估计第6年该市的个人年平均收入(保留三位有效数字).
年份x | 1 | 2 | 3 | 4 | 5 |
收入y(千元) | 21 | 24 | 27 | 29 | 31 |
其中![]() ,
,![]() ,
,![]() 附1:
附1:![]() =
= ![]() ,
,![]() =
=![]() ﹣
﹣![]()
![]()
(Ⅱ)下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表:
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表,并回答:能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”.
附2:
P(K2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3:
K2=![]() .(n=a+b+c+d)
.(n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,△PBC为等边三角形,点O为BC的中点,AC⊥PB,平面PBC⊥平面ABC.

(1)求直线PB和平面ABC所成的角的大小;
(2)求证:平面PAC⊥平面PBC;
(3)已知E为PO的中点,F是AB上的点,AF=![]() AB.若EF∥平面PAC,求
AB.若EF∥平面PAC,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行理科、文科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.
分组 | 频数 | 频率 | 分组 | 频数 | 频率 | |
[135,150] | 8 | 0.08 | [135,150] | 4 | 0.04 | |
[120,135) | 17 | 0.17 | [120,135) | 18 | 0.18 | |
[105,120) | 40 | 0.4 | [105,120) | 37 | 0.37 | |
[90,105) | 21 | 0.21 | [90,105) | 31 | 0.31 | |
[75,90) | 12 | 0. 12 | [75,90) | 7 | 0.07 | |
[60,75) | 2 | 0.02 | [60,75) | 3 | 0.03 | |
总计 | 100 | 1 | 总计 | 100 | 1 |
理科 文科
(Ⅰ)根据数学成绩的频率分布表,求文科数学成绩的中位数的估计值;(精确到0.01)
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:
数学成绩 | 数学成绩<120分 | 合计 | |
理科 | |||
文科 | |||
合计 | 200 |
参考公式与临界值表: ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com