
【题目】小金同学在学校中贯彻着“边玩边学”的学风,他在“汉诺塔”的游戏中发现了数列递推的奥妙:有![]() 、
、![]() 、
、![]() 三个木桩,
三个木桩,![]() 木桩上套有编号分别为
木桩上套有编号分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到
的七个圆环,规定每次只能将一个圆环从一个木桩移动到另一个木桩,且任意一个木桩上不能出现“编号较大的圆环在编号较小的圆环之上”的情况,现要将这七个圆环全部套到![]() 木桩上,则所需的最少次数为( )
木桩上,则所需的最少次数为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() 的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为 ![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某种书籍每册的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
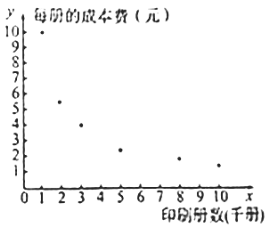
其中![]() ,
,![]() .
.
为了预测印刷![]() 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷
的回归方程,并预测印刷![]() 千册时每册的成本费.
千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: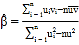 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() .点
.点![]() 是
是![]() 上的定点,
上的定点,![]() ,
,![]() 是
是![]() 上的两动点,且线段
上的两动点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
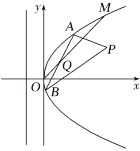
(Ⅰ)求曲线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)记![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
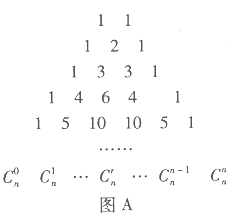
【题目】在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图![]() 所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”
所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”![]() ,如图
,如图![]() .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图
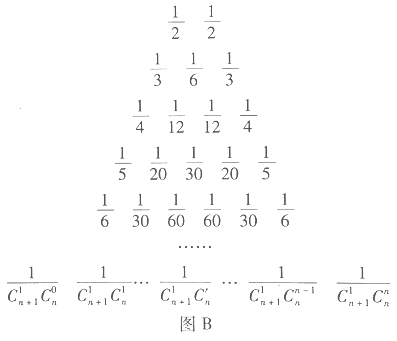
.17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图![]() .在杨辉三角中,相邻两行满足关系式:
.在杨辉三角中,相邻两行满足关系式:![]() ,其 中
,其 中![]() 是行数,
是行数,![]() .请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
.请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)设全集U=A∪B,求(UA)∪(UB);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com