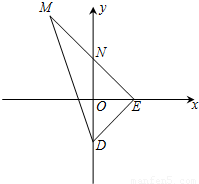
分析:(Ⅰ)设M(x,y),E(a,0),则D(0,-8),N(
,y),利用
⊥,N在y轴上,化简可得点F的轨迹方程;
(Ⅱ)设A(x
1,y
1),B(x
2,y
2),C(x
3,y
3),D(x
4,y
4),直线l
1,l
2的方程分别与抛物线方程联立,消去x可得,利用韦达定理,结合
•=
(+)•(+),利用基本不等式,即可求得结论.
解答:解:(Ⅰ)设M(x,y),E(a,0),则D(0,-8),N(
,y)
∵
⊥,N在y轴上,
∴(-a,-8)•(x-a,y)=-a(x-a)-8y=0且
=0∴2x
2-8y=0,所以点F的轨迹方程为x
2=4y(x≠0)…(6分)
(Ⅱ)设A(x
1,y
1),B(x
2,y
2),C(x
3,y
3),D(x
4,y
4),
直线l
1的方程为:y=kx+1(k≠0),则直线l
2的方程为
y=-x+1由y=kx+1与抛物线方程联立,消去x可得:y
2-(4k
2+2)y+1=0,则y
1+y
2=4k
2+2,y
1y
2=1
同理可得:y
3+y
4=
+2,y
3y
4=1
∴
•=
(+)•(+)=y
1y
2+y
3y
4+(y
1+y
2)+(y
3+y
4)+2=4(k
2+
)+4≥12,当且仅当k=±1时,取等号.
∴
•的最小值为12. …(12分)
点评:本题考查轨迹方程,考查直线与抛物线位置关系,考查向量知识的运用,考查基本不等式,联立方程,正确运用向量知识是关键.

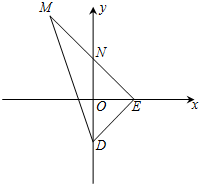 如图所示,在△DEM中,
如图所示,在△DEM中,

![]() ⊥
⊥![]() ,
,![]() =(0,-8),N在y轴上,且
=(0,-8),N在y轴上,且![]() =
=![]() (
(![]() +
+![]() ),点E在x轴上移动.
),点E在x轴上移动.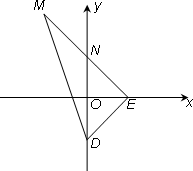
![]() ·
·![]() 的最小值.
的最小值.
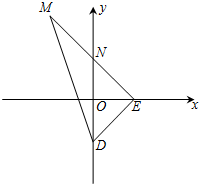 如图所示,在△DEM中,
如图所示,在△DEM中,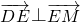 ,
, =(0,-8),N在y轴上,且DN=
=(0,-8),N在y轴上,且DN= (DE+DM),点E在x轴上移动.
(DE+DM),点E在x轴上移动.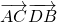 的最小值.
的最小值.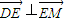 ,
,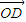 =(0,-8),N在y轴上,且DN=
=(0,-8),N在y轴上,且DN= (DE+DM),点E在x轴上移动.
(DE+DM),点E在x轴上移动.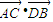 的最小值.
的最小值.