
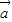 、
、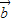 均为非零向量,则
均为非零向量,则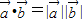 是
是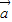 与
与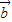 共线的条件是( )
共线的条件是( )科目:高中数学 来源: 题型:013
下列命题:
(1)如果非零向量 与
与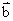 的方向相同或相反,那么
的方向相同或相反,那么 +
+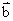 的方向必与
的方向必与 ,
,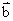 之一的方向相同.
之一的方向相同.
(2)△ABC中,必有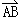 +
+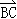 +
+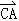 =
=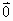 .
.
(3)若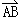 +
+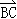 +
+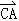 =
=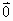 ,则A,B,C为一个三角形的三个顶点.
,则A,B,C为一个三角形的三个顶点.
(4)若 ,
,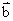 均为非零向量,则|
均为非零向量,则| +
+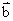 |与|
|与| |+|
|+|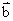 |一定相等.
|一定相等.
其中真命题的个数为
[ ]
查看答案和解析>>
科目:高中数学 来源:2006-2007年上学期华中师大一附中高三数学试题(附答案) 题型:013
下列命题中:(1)向量![]() 与
与![]() 是两个单位向量,则
是两个单位向量,则![]() 与
与![]() 相等;(2)在△ABC中,必有
相等;(2)在△ABC中,必有![]() ;(3)若
;(3)若![]() ,
,![]() 均为非零向量,则
均为非零向量,则![]() 与
与![]() 一定相等;(4)向量
一定相等;(4)向量![]() 与
与![]() 是共线向量,则点A、B、C、D必在同一条直线上;(5)若向量
是共线向量,则点A、B、C、D必在同一条直线上;(5)若向量![]() 与
与![]() 同向,且
同向,且![]() ,则
,则![]() .其中假命题的个数为
.其中假命题的个数为
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二第二学期期中考试文科数学试卷(解析版) 题型:选择题
若 、
、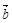 均为非零向量,则
均为非零向量,则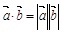 是
是 与
与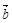 共线的( )
共线的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2007-2008学年贵州省遵义四中高二(下)期中数学试卷(理科)(解析版) 题型:选择题
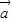 、
、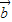 均为非零向量,则
均为非零向量,则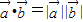 是
是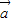 与
与 共线的条件是( )
共线的条件是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com