已知f(x)=(x-1)2,g(x)=4(x-1),f(an)和g(an)满足:a1=2,且(an+1-an)g(an)+f(an)=0.
(1)是否存在常数C,使得数列{an+C}为等比数列?若存在,证明你的结论;若不存在,请说明理由.
(2)设bn=3f(an)-[g(an+1)]2,求数列{bn}的前n项和Sn.
解:(1)由题意知:4(a
n+1-a
n)(a
n-1)+(a
n-1)
2=0
∴(a
n-1)(4a
n+1-3a
n-1)=0 …(2分)
∵a
1=2,∴a
n-1≠0,即4a
n+1=3a
n+1 …(4分)
假设存在常数C,使{a
n+C}为等比数列,
则:

为常数
∴c=-1,故存在常数c=-1,使{a
n-1}为等比数列…(6分)
(2)∵a
1=2,∴

,
∴

…(8分)
从而
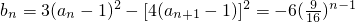
…(10分)
∴
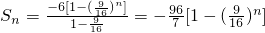
…(12分)
分析:(1)先根据 已知条件(a
n+1-a
n)g(a
n)+f(a
n)=0整理得到(a
n-1)(4a
n+1-3a
n-1)=0;再结合a
1=2,得到4a
n+1=3a
n+1;最后通过假设存在常数C,使{a
n+C}为等比数列,得到相邻两项的比值为常数求出常数c=-1;
(2)先根据第一问的 结果求出数列{a
n}的通项,再代入求出数列{b
n}的通项公式,最后根据等比数列的求和公式 即可得到结论.
点评:本题主要考查等比数列的求和公式的应用.再应用等比数列的求和公式时,一定要先判断公比是否等于1,避免出错.

 为常数
为常数 ,
, …(8分)
…(8分)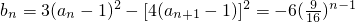 …(10分)
…(10分)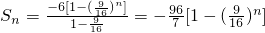 …(12分)
…(12分)

 已知f(x)=
已知f(x)= ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.