
【题目】定义在R上的奇函数f(x),当x∈(﹣∞,0)时,f(x)=﹣x2+mx﹣1.
(1)当x∈(0,+∞)时,求f(x)的解析式;
(2)若方程f(x)=0有五个不相等的实数解,求实数m的取值范围.
【答案】
(1)解:设x>0,则﹣x<0,∴f(﹣x)=﹣x2﹣mx﹣1
又f(x)为奇函数,即f(﹣x)=﹣f(x),
所以,f(x)=x2+mx+1(x>0),
又f(0)=0,
所以 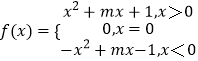
(2)解:因为f(x)为奇函数,所以函数y=f(x)的图象关于原点对称,
由方程f(x)=0有五个不相等的实数解,得y=f(x)的图象与x轴有五个不同的交点,
又f(0)=0,所以f(x)=x2+mx+1(x>0)的图象与x轴正半轴有两个不同的交点,
即,方程x2+mx+1=0有两个不等正根,记两根分别为x1,x2
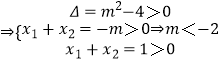 ,
,
所以,所求实数m的取值范围是m<﹣2
【解析】(1)先根据f(x)是定义在R上的奇函数,判断f(0)=0,再根据当x<0时,f(x)=﹣f(﹣x)根据x,0时,f(x)=﹣x2+mx﹣1得到x>0时函数的解析式,最后综合即可得到答案.(2)由方程f(x)=0有五个不相等的实数解,得y=f(x)的图象与x轴有五个不同的交点,又f(0)=0,所以f(x)=x2+mx+1(x>0)的图象与x轴正半轴有两个不同的交点即,方程x2+mx+1=0有两个不等正根,记两根分别为x1 , x2得出关于m的不等关系,从而求得实数m的取值范围.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】下列有关结论正确的个数为( )
①小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件![]() =“4个人去的景点不相同”,事件
=“4个人去的景点不相同”,事件![]() “小赵独自去一个景点”,则
“小赵独自去一个景点”,则![]() ;
;
②设函数![]() 存在导数且满足
存在导数且满足![]() ,则曲线
,则曲线![]() 在点
在点![]() 处的切线斜率为-1;
处的切线斜率为-1;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的值分别为
的值分别为![]() ;
;
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,(a>0).
,(a>0).
(1)当a=2时,证明函数f(x)不是奇函数;
(2)判断函数f(x)的单调性,并利用函数单调性的定义给出证明;
(3)若f(x)是奇函数,且f(x)﹣x2+4x≥m在x∈[﹣2,2]时恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数y=f(x),如果存在区间[m,n]D,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n]时,f(x)的值域也是[m,n].
则称[m,n]是该函数的“和谐区间”.
(1)证明:[0,1]是函数y=f(x)=x2的一个“和谐区间”.
(2)求证:函数 ![]() 不存在“和谐区间”.
不存在“和谐区间”.
(3)已知:函数 ![]() (a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n﹣m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣8≤0},B={x| ![]() <0},U=R.
<0},U=R.
(1)求A∪B;
(2)求(UA)∩B;
(3)如果C={x|x﹣a>0},且A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(II)设函数![]() 存在两个极值点,并记作
存在两个极值点,并记作![]() ,若
,若![]() ,求正数
,求正数![]() 的取值范围;
的取值范围;
(III)求证:当![]() =1时,
=1时, ![]() (其中e为自然对数的底数)
(其中e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在x=1处的切线与直线
在x=1处的切线与直线![]() 平行。
平行。
(Ⅰ)求a的值并讨论函数y=f(x)在![]() 上的单调性。
上的单调性。
(Ⅱ)若函数![]() (
(![]() 为常数)有两个零点
为常数)有两个零点![]() ,
,
(1)求m的取值范围;
(2)求证: ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量![]() (单位:粒,
(单位:粒, ![]() )的函数解析式
)的函数解析式![]() ;
;
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量![]() (单位:粒),整理得下表:
(单位:粒),整理得下表:
雕刻量 | 210 | 230 | 250 | 270 | 300 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天的收入不低于300元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com