
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人. 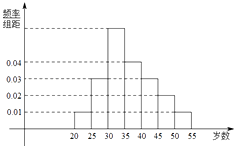
(1)求N和[30,35)这组的参加者人数N1;
(2)已知[30,35)和[35,40)这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学老师的概率;
(3)组织者从[45,55)这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为x,求x的分布列和均值.
【答案】
(1)解:∵年龄在[35,40)内的频率为0.04×5=0.2,
∴总人数N= ![]() =40人.
=40人.
∵[30,35)这组的频率为:1﹣(0.01×2+0.02+0.03×2+0.04)×5=0.3,
[30,35)这组的参加者人数N1为:40×0.3=12人
(2)解:记事件B为“从年龄在[30,35]之间选出的人中至少有2名数学教师”,
∵年龄在[30,35)之间的人数为12,
∴P(B)=1﹣ ![]() =
= ![]() ,
,
记事件C为“从年龄在[35,40)之间选出的人中至少有1名数学教师”,
∵年龄在[35,40)之间的人数为8,
∴P(C)=1﹣ ![]() =
= ![]() ,
,
∴两组选出的人中都至少有1名数学老师的概率P(BC)= ![]() =
= ![]()
(3)解:年龄在[45,55)之间的人数为6人,其中女教师4人,
∴ξ的可能取值为1,2,3,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 1 | 2 | 3 |
P |
|
|
|
Eξ= ![]() =2
=2
【解析】(1)先求出年龄在[35,40)内的频率,由此能求出总人数和[30,35)这组的参加者人数N1 . (2)记事件B为“从年龄在[30,35]之间选出的人中至少有1名数学教师”,记事件C为“从年龄在[35,40)之间选出的人中至少有1名数学教师”,分别求出P(B),P(C),由此能求出两组选出的人中都至少有1名数学老师的概率.(3)年龄在[45,55)之间的人数为6人,其中女教师4人,ξ的可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
【考点精析】本题主要考查了频率分布直方图和离散型随机变量及其分布列的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为( ![]() ,
, ![]() ),直线l的极坐标方程为ρcos(θ﹣
),直线l的极坐标方程为ρcos(θ﹣ ![]() )=a,且点A在直线l上,
)=a,且点A在直线l上,
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为 ![]() (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最新公布的《道路交通安全法》和《道路交通安全法实施条例》对车速、安全车距以及影响驾驶人反应快慢等因素均有详细规定,这些规定说到底主要与刹车距离有关,刹车距离是指从驾驶员发现障碍到制动车辆,最后完全停止所行驶的距离,即:刹车距离=反应距离+制动距离,反应距离=反应时间×速率,制动距离与速率的平方成正比,某反应时间为![]() 的驾驶员以
的驾驶员以![]() 的速率行驶,遇紧急情况,汽车的刹车距离为
的速率行驶,遇紧急情况,汽车的刹车距离为![]() .
.
(![]() )试将刹车距离
)试将刹车距离![]() 表示为速率
表示为速率![]() 的函数.
的函数.
(![]() )若该驾驶员驾驶汽车在限速为
)若该驾驶员驾驶汽车在限速为![]() 的公路上行驶,遇紧急情况,汽车的刹车距离为
的公路上行驶,遇紧急情况,汽车的刹车距离为![]() ,试问该车是否超速?请说明理由.
,试问该车是否超速?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() 是圆
是圆![]() 上的一个动点,
上的一个动点,![]() 的中垂线
的中垂线![]() 交
交![]() 于点
于点![]() ,以直线
,以直线![]() 为
为![]() 轴,
轴,![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系。
轴建立平面直角坐标系。

(Ⅰ)若点![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)设点![]() 为圆
为圆![]() 上任意一点,过
上任意一点,过![]() 作圆
作圆![]() 的切线与曲线
的切线与曲线![]() 交于
交于![]() 两点,证明:以
两点,证明:以![]() 为直径的圆经过定点,并求出该定点的坐标。
为直径的圆经过定点,并求出该定点的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
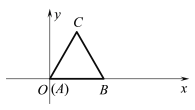
【题目】如图放置的边长为2的正三角形ABC沿x轴滚动,记滚动过程中顶点A的横、纵坐标分别为![]() 和
和![]() ,且
,且![]() 是
是![]() 在映射
在映射![]() 作用下的象,则下列说法中:
作用下的象,则下列说法中:
① 映射![]() 的值域是
的值域是![]() ;
;
② 映射![]() 不是一个函数;
不是一个函数;
③ 映射![]() 是函数,且是偶函数;
是函数,且是偶函数;
④ 映射![]() 是函数,且单增区间为
是函数,且单增区间为![]() ,
,
其中正确说法的序号是___________.
说明:“正三角形ABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点B为中心顺时针旋转,当顶点C落在x轴上时,再以顶点C为中心顺时针旋转,如此继续.类似地,正三角形ABC可以沿x轴负方向滚动.
查看答案和解析>>
科目:高中数学 来源: 题型:
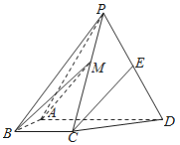
【题目】如图,四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 中点.
中点.
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]()
![]() 平面
平面![]() ,
, ![]() 与
与![]() 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形, ![]() //
// ![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() //
// ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的重心,
的重心, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() //平面
//平面![]() ;
;
(Ⅱ)若直线![]() 与
与![]() 所成角为
所成角为![]() ,试求二面角
,试求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com