
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益M、养鸡的收益N与投入a(单位:万元)满足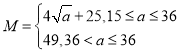 ,N=
,N=![]() a+20.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
a+20.设甲合作社的投入为x(单位:万元),两个合作社的总收益为f(x)(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作社的投入,才能使总收益最大,最大总收益为多少万元?
【答案】(1)88.5万元
(2)该公司在甲合作社投入16万元,在乙合作社投入56万元,总收益最大,最大总收益为89万元
【解析】
根据题意,当甲合作社投入为25万元时,乙合作社投入为47万元,分别代入其收益与投入的函数式,最后求和即可。
首先确定函数定义域,然后结合分段函数的解析式分类讨论确定最大收益的安排方法即可得出答案。
解:(1)当甲合作社投入为25万元时,乙合作社投入为47万元,此时两个个合作社的总收益为:
![]() =88.5(万元);
=88.5(万元);
(2)甲合作社的投入为x万元(15≤x≤57),则乙合作社的投入为72﹣x万元,
当15≤x≤36时,则36≤72﹣x≤57,
f(x)=4![]() +25+
+25+![]() (72﹣x)+20=﹣
(72﹣x)+20=﹣![]() x+4
x+4![]() +81.
+81.
令t=![]() ,得
,得![]() ≤t≤6,
≤t≤6,
则总收益为g(t)=﹣![]() t2+4t+81=﹣
t2+4t+81=﹣![]() (t﹣4)2+89,
(t﹣4)2+89,
显然当t=4时,函数取得最大值g(t)=89=f(16),
即此时甲投入16万元,乙投入56万元时,总收益最大,最大收益为89万元
当36<x≤57时,则15<72﹣x≤36,
则f(x)=49+![]() (72﹣x)+20=﹣
(72﹣x)+20=﹣![]() x+105,
x+105,
则f(x)在(36,57]上单调递减,
∴f(x)<f(36)=87.
即此时甲、乙总收益小于87万元.
又89>87,
∴该公司在甲合作社投入16万元,在乙合作社投入56万元,总收益最大,最大总收益为89万元.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】为了了解我市参加2018年全国高中数学联赛的学生考试结果情况,从中选取60名同学将其成绩(百分制,均为正数)分成![]() 六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形,回答下列问题:
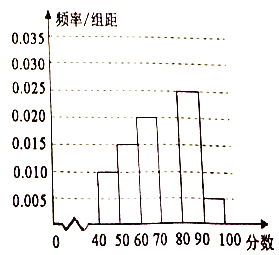
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1≤x≤3},B={x|x>2}.
(Ⅰ)分别求A∩B,(RB)∪A;
(Ⅱ)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是平行四边形
是平行四边形![]() 所在平面外一点,如果
所在平面外一点,如果![]() ,
,![]() ,
,![]() .(1)求证:
.(1)求证:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四边形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意结合空间向量数量积的运算法则计算可得![]() ,
,![]() .则
.则![]() ,
,![]() ,结合线面垂直的判断定理可得
,结合线面垂直的判断定理可得![]() 平面
平面![]() ,即
,即![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)利用平面向量的坐标计算可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
试题解析:
(1)∵![]() ,
,
![]() .
.
∴![]() ,
,![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的法向量.
的法向量.
(2)∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,![]()
![]() .
.
【题型】解答题
【结束】
19
【题目】(1)求圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() 的圆的方程;
的圆的方程;
(2)求与圆![]() 外切于点
外切于点![]() 且半径为
且半径为![]() 的圆的方程.
的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=3x![]() .
.
(1)若f(x)=8,求x的值;
(2)对于任意的x∈[0,2],[f(x)-3]3x+13-m≥0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若![]() 是
是![]() 上的有界函数,且
上的有界函数,且![]() 的上界为3,求实数
的上界为3,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河南濮阳市高三一模】已知点![]() 在抛物线
在抛物线![]() 上,
上, ![]() 是抛物线上异于
是抛物线上异于![]() 的两点,以
的两点,以![]() 为直径的圆过点
为直径的圆过点![]() .
.
(I)证明:直线![]() 过定点;
过定点;
(II)过点![]() 作直线
作直线![]() 的垂线,求垂足
的垂线,求垂足![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com