已知倾斜角为135°且过点（2，1）的直线l与圆C：（x-1）2+y2=4相交与A，B两点，
（1）求直线l的方程；
（2）求弦长|AB|．
【答案】
分析：（1）因为直线l倾斜角为135°且经过点（2，1），求出直线的斜率，根据直线的点斜式方程，即可求得结果；
（2）利用垂径定理及勾股定理，由圆的半径r及圆心到直线的距离d，即可求出|AB|的长．
解答：解（1）依题有直线l的斜率为k=tan135°=-1，又直线l过点（2，1），
所以直线l的方程为：y-1=-1（x-2），
即：x+y-3=0．
（2）圆心（1，0）到直线x+y-3=0的距离为：
，
又圆的半径为2，所以|AB|=
．
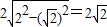
点评：此题考查学生掌握并灵活运用直线与圆的方程，利用运用圆的垂径定理、勾股定理及韦达定理化简求值，是一道综合题，考查运算能力，是基础题．
