
 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠IOA=60°,设$\overrightarrow{OD}$=$\overrightarrow{a}$,$\overrightarrow{OH}$=$\overrightarrow{b}$,已知点P在各菱形边上运动,且$\overrightarrow{OP}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,x,y∈R,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠IOA=60°,设$\overrightarrow{OD}$=$\overrightarrow{a}$,$\overrightarrow{OH}$=$\overrightarrow{b}$,已知点P在各菱形边上运动,且$\overrightarrow{OP}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,x,y∈R,则x+y的最大值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 可以O为坐标原点,GC所在直线为x轴,建立平面直角坐标系,可设菱形的边长为2,从而能求出D,H点的坐标,这样便可得到向量$\overrightarrow{a},\overrightarrow{b}$的坐标.可设P(X,Y),根据条件即可得出$x+y=\frac{2\sqrt{3}}{3}Y-X$,这样设x+y=z,X,Y的活动域便是菱形的边上,这样根据线性规划的知识即可求出z的最大值,即求出x+y的最大值.
解答  解:如图,以GC所在直线为x轴,过O且垂直于GC的直线为y轴,建立如图所示坐标系,设菱形的边长为2,则:
解:如图,以GC所在直线为x轴,过O且垂直于GC的直线为y轴,建立如图所示坐标系,设菱形的边长为2,则:
D($1,\sqrt{3}$),H($-3,-\sqrt{3}$);
设P(X,Y),则(X,Y)=x($1,\sqrt{3}$)+y($-3,-\sqrt{3}$);
∴$\left\{\begin{array}{l}{X=x-3y}\\{Y=\sqrt{3}x-\sqrt{3}y}\end{array}\right.$;
∴$x+y=\frac{2\sqrt{3}}{3}Y-X$;
设$z=\frac{2\sqrt{3}}{3}Y-X$;
∴$Y=\frac{\sqrt{3}}{2}X+\frac{\sqrt{3}}{2}z$,$\frac{\sqrt{3}}{2}z$表示在y轴上的截距;
∴当截距最大时,z取到最大值;
根据图形可看出,当直线经过点E($0,2\sqrt{3}$)时,截距最大;
∴$2\sqrt{3}=0+\frac{\sqrt{3}}{2}z$;
z=4;
∴x+y的最大值为4.
故选B.
点评 考查建立平面直角坐标系,利用向量坐标解决向量问题的方法,能求平面上点的坐标,掌握这种引入变量X,Y来表示x+y,从而求x+y最值的方法,利用线性规划求最值的方法及过程.


科目:高中数学 来源: 题型:选择题
| A. | M?N | B. | M?N | C. | M∩N=∅ | D. | M=N |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
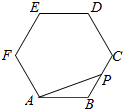 如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].
如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在等腰梯形ABCD中,∠A=$\frac{π}{3}$,边AB、DC的长分别为2、1,若M、N分别是边BC、CD上的点,且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是( )
在等腰梯形ABCD中,∠A=$\frac{π}{3}$,边AB、DC的长分别为2、1,若M、N分别是边BC、CD上的点,且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是( )| A. | [$\frac{3}{2}$,+∞) | B. | (0,2] | C. | [$\frac{3}{2}$,3] | D. | ($\frac{3}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com