练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分11分）设函数f (x)＝x3－x2＋ax．

    (Ⅰ)函数f (x)在（11, 2012）内单调递减，求a范围；

    (Ⅱ) 若实数a满足1＜a≤2，函数g(x)＝4x3＋3bx2－6(b＋2)x (b∈R) 的极小值点与f (x)的极小值点相同，求证：g(x)的极大值小于等于10．

     

     

     

     

     

     

     

     

     

     

     

     

     

    (Ⅰ) 解：f ′(x)＝x2－(a＋1)x＋a＝(x－1)(x－a)．

    由题意2012≤a…………4分【其他方法酌情给分】

    (Ⅱ) (Ⅱ) 解：f ′(x)＝x2－(a＋1)x＋a＝(x－1)(x－a)．

    由于a＞1，所以f (x)的极小值点x＝a，则g(x)的极小值点也为x＝a．……6分

    而g ′ (x)＝12x2＋6bx－6(b＋2)＝6(x－1)(2x＋b＋2)，所以，

    即b＝－2(a＋1)．又因为1＜a≤2，……8分

    所以  g(x)极大值＝g(1)＝4＋3b－6(b＋2)＝－3b－8＝6a－2≤10．

    故g(x)的极大值小于等于10．…………………………11分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    本题（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．
    （1）选修4-2：矩阵与变换
    已知矩阵A=
    33
    cd
    ，若矩阵A属于特征值6的一个特征向量为
    α
    =
    1
    1
    ，属于特征值1的一个特征向量为
    β
    =
    ^ 
    &-2    ；
    （Ⅰ）求矩阵A；
    （Ⅱ）判断矩阵A是否可逆，若可逆求出其逆矩阵A-1．
    （2）选修4-4：坐标系与参数方程
    已知直线的极坐标方程为ρsin(θ+
    π
    4
    )=
    		2
    2
    ，圆M的参数方程为
    x=2cosθ
    y=-2+2sinθ
    （其中θ为参数）．
    （Ⅰ）将直线的极坐标方程化为直角坐标方程；
    （Ⅱ）求圆M上的点到直线的距离的最小值．
    （3）选修4-5：不等式选讲，设函数f（x）=|x-1|+|x-a|；
    （Ⅰ）若a=-1，解不等式f（x）≥3；
    （Ⅱ）如果关于x的不等式f（x）≤2有解，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广东省广州市高三上学期第3次月考理科数学试卷（解析版） 题型：解答题

    把正奇数数列中的数按上小下大、左小右大的原则排成如下三角形数表：

    1

    3    5

    7    9   11

    ………………………

    ……………………………

    设是位于这个三角形数表中从上往下数第行、从左往右数第个数．

    （1）若，求的值；

    （2）若记三角形数表中从上往下数第行各数的和为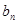，求证．（本题满分14分）

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年甘肃省高三第二次诊断性考试理科数学试卷 题型：解答题

    （本题满分12分）已知数列{an}的前n项和为Sn，点(n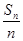，)在直线y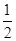＝x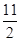＋上．数列{bn}满足bn＋2－2bn＋1＋bn＝0(n∈N*)，b3＝11，且其前9项和为153.

    (1)求数列{an}，{bn}的通项公式；

    (2)设cn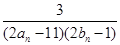＝，数列{cn}的前n项和为Tn，求使不等式Tn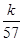＞对一切n∈N*都成立的最大正整数k的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省高三十一月份阶段性考试理科数学 题型：解答题

    （本题满分12分）

    已知数列{an}的前n项和为Sn，点(n，)在直线y＝x＋上．数列{bn}满足bn＋2－2bn＋1＋bn＝0(n∈N*)，b3＝11，且其前9项和为153.

    (1)求数列{an}，{bn}的通项公式；

    (2)设cn＝，数列{cn}的前n项和为Tn，求使不等式Tn＞对一切n∈N*都成立的最大正整数k的值．

     

    查看答案和解析>>

    同步练习册答案