
【题目】已知函数![]() .
.
(1)求证:函数![]() 有唯一零点;
有唯一零点;
(2)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)求出![]() ,先证明
,先证明![]() 在区间
在区间![]() 上为增函数,又
上为增函数,又![]() ,
,![]() ,所以
,所以![]() 在区间
在区间![]() 上恰有一个零点,而
上恰有一个零点,而![]() 在
在![]() 上恒成立,在
上恒成立,在![]() 上无零点,从而可得结果;(2))设
上无零点,从而可得结果;(2))设![]() 的零点为
的零点为![]() ,即
,即![]() . 原不等式可化为
. 原不等式可化为![]() ,令
,令![]() 若
若![]() ,可得
,可得![]() ,等式左负右正不相等,若
,等式左负右正不相等,若![]() ,等式左正右负不相等,只能
,等式左正右负不相等,只能![]() ,
,![]() ,即
,即![]() 求所求.
求所求.
试题解析:(1)![]() ,
,
易知![]() 在
在![]() 上为正,因此
上为正,因此![]() 在区间
在区间![]() 上为增函数,又
上为增函数,又![]() ,
,![]()
因此![]() ,即
,即![]() 在区间
在区间![]() 上恰有一个零点,
上恰有一个零点,
由题可知![]() 在
在![]() 上恒成立,即在
上恒成立,即在![]() 上无零点,
上无零点,
则![]() 在
在![]() 上存在唯一零点.
上存在唯一零点.
(2)设![]() 的零点为
的零点为![]() ,即
,即![]() . 原不等式可化为
. 原不等式可化为![]() ,
,
令![]() ,则
,则![]() ,由(1)可知
,由(1)可知![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,故只求
上单调递增,故只求![]() ,,设
,,设![]() ,
,
下面分析![]() ,设
,设![]() ,则
,则![]() ,
,
可得![]() ,即
,即![]()
若![]() ,等式左负右正不相等,若
,等式左负右正不相等,若![]() ,等式左正右负不相等,只能
,等式左正右负不相等,只能![]() .
.
因此![]() ,即
,即![]() 求所求.
求所求.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 在倾斜角为
在倾斜角为![]() 的直线
的直线![]() 上,以坐标原点
上,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)写出![]() 的参数方程及
的参数方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
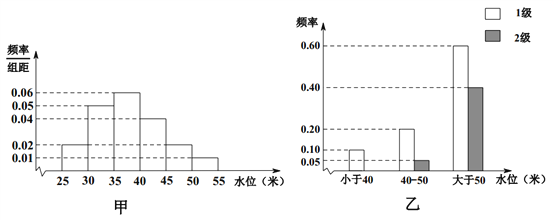
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,
,![]() 与
与![]() 交于另一点为
交于另一点为![]() .若以点
.若以点![]() 为圆心,以线段
为圆心,以线段![]() 长为半径的圆与
长为半径的圆与![]() 有4个公共点,求
有4个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若满足条件:存在
,若满足条件:存在![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则称
,则称![]() 为“倍缩函数”.若函数
为“倍缩函数”.若函数![]() 为“倍缩函数”,则实数
为“倍缩函数”,则实数![]() 的取值范围是
的取值范围是
A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高黔东南州的整体旅游服务质量,州旅游局举办了黔东南州旅游知识竞赛,参赛单位为本州内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游3名,其中高级导游1名.从这6名导游中随机选择2人 参加比赛.
(Ⅰ)求选出的2人都是高级导游的概率;
(Ⅱ)为了进一步了解各旅游协会每年对本地经济收入的贡献情况,经多次统计得到,甲旅游协会对本地经济收入的贡献范围是![]() (单位:万元),乙旅游协会对本地经济收入的贡献范围是
(单位:万元),乙旅游协会对本地经济收入的贡献范围是![]() (单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献的概率.
(单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知直角梯形ABCD中,![]() ,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
(Ⅰ)求证:平面PAE⊥平面ABCE;
(Ⅱ)求点B到平面PCE的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com