
【题目】设数列{an}的前n项和为Sn , 且Sn=n2﹣4n﹣5
(1)求数列{an}的通项公式;
(2)设bn=|an|,数列{bn}的前n项和为Tn, 求Tn .
【答案】(1)![]() (2)
(2)
【解析】
(1)由Sn=n2﹣4n﹣5,可得当n≥2时,an=Sn﹣Sn﹣1=2n﹣5,再检验当n=1时,a1是否适合上式,即可求得数列{an}的通项公式;
(2)由bn=|an|=|2n﹣5|,分n=1、n=2、n≥3三类讨论,分别求得数列{bn}的前n项和Tn,最后综合起来即可求.
(1)解:∵Sn=n2﹣4n﹣5,
∴当n≥2时,an=Sn﹣Sn﹣1=n2﹣4n﹣5﹣[(n﹣1)2﹣4(n﹣1)﹣5]=2n﹣5,
又当n=1时,a1=﹣8不适合上式,
∴![]()
(2)解:∵bn=|an|,数列{bn}的前n项和为Tn,
当n=1时,b1=|a1|=8,T1=8;
当n=2时,b2=|a2|=1,T2=8+1=9;
∵n≥3时,an=2n﹣5≥1>0,
∴bn=|an|=an=2n﹣5,
∴Tn=8+1+(1+3+…+2n﹣5)=9+ ![]() =(n﹣2)2+9=n2﹣4n+13.
=(n﹣2)2+9=n2﹣4n+13.
综上, 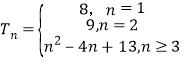


科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}满足a1=1,且a1 , a2 , a5成等比数列.
(1)求{an}的通项公式;
(2)若bn=(﹣1)n ![]() (n∈N*),求数列{bn}的前n项和Sn .
(n∈N*),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD-A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个车间为了规定工时定额,需要确定加工某种零件所花费的时间,为此进行了6次试验,收集数据如下:
零件数 |
|
|
|
|
|
|
加工时间 |
|
|
|
|
|
|
(Ⅰ)在给定的坐标系中划出散点图,并指出两个变量是正相关还是负相关;
(Ⅱ)求回归直线方程;
(Ⅲ)试预测加工![]() 个零件所花费的时间?
个零件所花费的时间?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:

 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点为
)的左焦点为![]() ,左准线方程为
,左准线方程为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
①若直线![]() 经过椭圆
经过椭圆![]() 的左焦点
的左焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() ,
, ![]() .求证:
.求证: ![]() 为定值;
为定值;
②若![]() (
(![]() 为原点),求
为原点),求![]() 面积的取值范围.
面积的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com