分析:由已知可得
=2
,即点M是线段AB的中点,可判断①的真假;由已知可得
=2
,故M,A,B三点共线,可判断②的真假;根据
表示与
同向的单位向量,可得M点是以
同向的单位向量和又
同向的单位向量为两邻边的菱形对角线顶点上,进而根据菱形的性质,可判断③的真假;由已知可得
+
+
=
,可得M为三角形的重心,进而判断④的真假;根据已知分析点M在△OAB外的各种情况,综合讨论结果,可得答案.
解答:解:当
λ=,μ=时,
=+,此时
=
-
,
=
-
=
-+,故
=2
,即点M是线段AB的中点,故①正确;
当λ=-1,μ=2时,
=-+2,此时
=
-
,
=
-
=
-2+2=2
,故M,A,B三点共线,故②正确;
当
λ=,μ=时,
=+,此时M点是以
同向的单位向量和又
同向的单位向量为两邻边的菱形对角线顶点上,根据菱形对角线平分对角,可得点M在∠AOB的平分线上,故③正确;
当
λ=,μ=时,
=+,此时
+
+
=
,可得M为三角形的重心,故④正确;
反向延长OA,OB,分别计为OC,OD,当M点在区域AOC上时,λ<0;当M点在区域BOD上时,μ<0;当M点在区域COD上时,λ<0且μ<0;当M点在区域COD上时,λ>0且μ>0,若此时M点△OAB外,则
,故⑤正确
故答案为:①②③④⑤
点评:本题又命题的真假判断为载体考查了向量的性质,是向量问题的综合应用,难度稍大,属中档题.



 名校课堂系列答案
名校课堂系列答案![]() (如图2所示).那么对于图中给定的
(如图2所示).那么对于图中给定的![]() ,下列判断中一定正确的是
,下列判断中一定正确的是![]() 时刻,甲车在乙车前面 w.w.w.k.s.5.u.c.o.m
时刻,甲车在乙车前面 w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() 时刻后,甲车在乙车后面
时刻后,甲车在乙车后面![]() 时刻,两车的位置相同
时刻,两车的位置相同![]() 时刻后,乙车在甲车前面
时刻后,乙车在甲车前面
 ,则下列命题正确的是 .(写出所有正确命题的编号)
,则下列命题正确的是 .(写出所有正确命题的编号)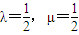 ,则点M是线段AB的中点;
,则点M是线段AB的中点;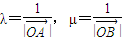 ,则点M在∠AOB的平分线上;
,则点M在∠AOB的平分线上;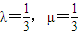 ,则点M是△OAB的重心;
,则点M是△OAB的重心;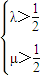 .
.