
【题目】在等腰梯形![]() 中,
中,![]() ,直线
,直线![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)见解析(2)见解析(3) ![]()
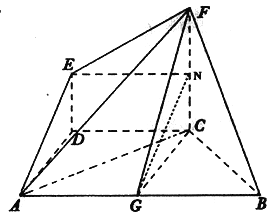
【解析】分析:(1)取FC中点N,连接EN,推导出四边形EDCN是平行四边形,从而EN![]() DC,连接NG,推导出四边形EAGN是平行四边形,从而EA∥NG,由此能证明AE∥平面GCF.
DC,连接NG,推导出四边形EAGN是平行四边形,从而EA∥NG,由此能证明AE∥平面GCF.
(2)由DC![]() AG,得四边形AGCD为平行四边形,从而AD=GC,推导出AC⊥BC,AC⊥CF,从而AC⊥平面BCF,由此能证明平面ACF⊥平面BCF.
AG,得四边形AGCD为平行四边形,从而AD=GC,推导出AC⊥BC,AC⊥CF,从而AC⊥平面BCF,由此能证明平面ACF⊥平面BCF.
(3)推导出ED∥平面GCF,AE∥平面GCF,从而平面ADE∥平面GCF,进而直线FB与平面ADE所成角也为直线FB与平面GCF所成角.由此能求出直线FB与平面ADF所成角正弦值.
详解:(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() 平行且等于
平行且等于![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() 平行且等于
平行且等于![]() ,
,
连接![]() 平行且等于
平行且等于![]() ,又
,又![]() 平行且等于
平行且等于![]() ,
,
所以![]() 平行且等于
平行且等于![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)∵![]() 平行且等于
平行且等于![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 为等边三角形,
为等边三角形,
∵![]() ,
,
∴![]() ,由余弦定理得
,由余弦定理得
![]() ,
,
所以![]() 即
即![]() ,
,
所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(3)因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
由(1)知![]() 平面
平面![]() ,且
,且![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角也为直线
所成角也为直线![]() 与平面
与平面![]() 所成角.
所成角.
由(2)知![]() ,设
,设![]() 为
为![]() 中点,连接
中点,连接![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,
所成角,
因为![]() ,
,
在直角![]() 中,
中,![]() ,
,![]()
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() ,
,![]() ,C与l有且仅有一个公共点.
,C与l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)O为极点,A,B为C上的两点,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上恰有2个零点,求
上恰有2个零点,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,若
时,若![]() 对任意的正整数
对任意的正整数![]() 在区间
在区间![]() 上始终存在
上始终存在![]() 个整数使得
个整数使得![]() 成立,试问:正整数
成立,试问:正整数![]() 是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:
使用年数 |
|
|
|
|
|
|
售价 |
|
|
|
|
|
|
|
|
|
|
|
|
|
下面是![]() 关于
关于![]() 的折线图:
的折线图:

(1)由折线图可以看出,可以用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的回归方程并预测某辆
的回归方程并预测某辆![]() 型号二手车当使用年数为
型号二手车当使用年数为![]() 年时售价约为多少?(
年时售价约为多少?(![]() 、
、![]() 小数点后保留两位有效数字)
小数点后保留两位有效数字)
(3)基于成本的考虑,该型号二手车的售价不得低于![]() 元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考数据:
![]() ,
,![]() ,
,![]() ,
,
 ,
, ,
,
 ,
,![]() ,
,![]() .
.
参考公式:回归直线方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
 ,
,![]() 、
、![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求直线![]() l的普通方程和曲线
l的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com