
·ÖĪö £Ø1£©ĄūÓĆŹżĮŠ{an}¾ßÓŠŠŌÖŹPµÄøÅÄī£¬¶ŌŹżĮŠ{xn}£ŗ-2£¬2ÓėŹżĮŠ{xn}£ŗ-2£¬-1£¬1£¬3·ÖĪöÅŠ¶Ļ¼“æÉ£»Č”A1£Øxi£¬xi£©£¬ŹżĮŠ{xn}¾ßÓŠŠŌÖŹP£¬¹Ź“ęŌŚµćA2£Øxi£¬xj£©Ź¹µĆOA1”ĶOA2£¬ĄūÓĆĻņĮæµÄ×ų±źŌĖĖćÕūĄķ¼“æÉÖ¤µĆxi+xj=0£»ŹżĮŠ{xn}ÖŠŅ»¶Ø“ęŌŚĮ½Ļīxi£¬xjŹ¹µĆxi+xj=0£»ŹżĮŠ{xn}ŹĒµ„µ÷µŻŌöŹżĮŠĒŅx2£¾0£¬1ĪŖŹżĮŠ{xn}ÖŠµÄŅ»Ļī£¬Ķعż·“Ö¤·ØæÉÖ¤µĆx2=1£»
£Ø2£©x2=1£®ČōŹżĮŠ{xn}Ö»ÓŠ2015ĻīĒŅ¾ßÓŠŠŌÖŹP£¬æɵĆx4=4£¬x5=8£¬²ĀĻėŹżĮŠ{xn}“ÓµŚ¶žĻīĘšŹĒ¹«±ČĪŖ2µÄµČ±ČŹżĮŠ£¬ĄūÓƵȱȏżĮŠµÄĒóŗĶ¹«Ź½¼ĘĖć¼“æÉ£®
½ā“š ½ā£ŗ£Ø1£©¢Ł¶ŌÓŚŹżĮŠ{xn}£¬ČōA1£Ø-2£¬2£©£¬ŌņA2£Ø2£¬2£©£¬
ČōA1£Ø-2£¬-2£©ŌņA2£Ø2£¬-2£©£¬¾łĀś×ćOA1”ĶOA2£¬ĖłŅŌ¢Ł¾ßÓŠŠŌÖŹP£¬¹Ź¢ŁÕżČ·£»
¢Ś¶ŌÓŚŹżĮŠ{xn}£¬µ±A1£Ø-2£¬3£©Čō“ęŌŚA2£Øx£¬y£©Āś×ćOA1”ĶOA2£¬
¼“-2x+3y=0£¬¼“$\frac{y}{x}$=$\frac{2}{3}$£¬ŹżĮŠ{xn}ÖŠ²»“ęŌŚÕāŃłµÄŹżx£¬y£¬Ņņ“Ė¢Ś²»¾ßÓŠŠŌÖŹP£¬¹Ź¢Ś²»ÕżČ·£»
¢ŪČ”A1£Øxi£¬xi£©£¬ÓÖŹżĮŠ{xn}¾ßÓŠŠŌÖŹP£¬ĖłŅŌ“ęŌŚµćA2£Øxi£¬xj£©Ź¹µĆOA1”ĶOA2£¬
¼“xixi+xixj=0£¬ÓÖxi”Ł0£¬ĖłŅŌxi+xj=0£¬¹Ź¢ŪÕżČ·£»
¢ÜÓÉ¢ŪÖŖ£¬ŹżĮŠ{xn}ÖŠŅ»¶Ø“ęŌŚĮ½Ļīxi£¬xjŹ¹µĆxi+xj=0£»
ÓÖŹżĮŠ{xn}ŹĒµ„µ÷µŻŌöŹżĮŠĒŅx2£¾0£¬ĖłŅŌ1ĪŖŹżĮŠ{xn}ÖŠµÄŅ»Ļī£®
¼ŁÉčx2”Ł1£¬Ōņ“ęŌŚk£Ø2£¼k£¼n£¬k”ŹN*£©ÓŠxk=1£¬ĖłŅŌ0£¼x2£¼1£®
“ĖŹ±Č”A1£Øx2£¬xn£©£¬ŹżĮŠ{xn}¾ßÓŠŠŌÖŹP£¬ĖłŅŌ“ęŌŚµćA2£Øxi£¬xs£©Ź¹µĆOA1”ĶOA2£¬
ĖłŅŌx2xi+xnxs=0£»Ö»ÓŠx1£¬ĖłŅŌµ±x1=-1Ź±x2=xnxs£¾xs”Żx2£¬Ć¬¶Ü£»
µ±xs=-1Ź±x2=$\frac{{x}_{n}}{{x}_{i}}$”Ż1£¬Ć¬¶Ü£®ĖłŅŌx2=1£¬¹Ź¢ÜÕżČ·£®
£Ø2£©ÓÉ£Ø1£©ÖŖ£¬x2=1£®ČōŹżĮŠ{xn}Ö»ÓŠ2015ĻīĒŅ¾ßÓŠŠŌÖŹP£¬æɵĆx4=4£¬x5=8£¬
²ĀĻėŹżĮŠ{xn}“ÓµŚ¶žĻīĘšŹĒ¹«±ČĪŖ2µÄµČ±ČŹżĮŠ£¬ĖłŅŌS2015=-1+1+2+4+”+22015
=2+4+”+22015=22016-2£®
¹Ź“š°øĪŖ£ŗ¢Ł¢Ū¢Ü£»22016-2£®
µćĘĄ ±¾Ģāæ¼²éµČ²īŹżĮŠÓėµČ±ČŹżĮŠµÄ×ŪŗĻ£¬æ¼²éŠĀøÅÄīµÄĄķ½āÓėÓ¦ÓĆ£¬Ķ»³öæ¼²é³éĻóĖ¼Ī¬Óė·“Ö¤·ØµÄ×ŪŗĻÓ¦ÓĆ£¬ŹōÓŚÄŃĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $£Ø3+4\sqrt{2}£¬+”Ž£©$ | B£® | $£Ø2\sqrt{2}-1£¬+”Ž£©$ | C£® | $£Ø0£¬2\sqrt{2}-1£©$ | D£® | $£Ø0£¬3+4\sqrt{2}£©$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | ³ä·Ö²»±ŲŅŖĢõ¼ž | B£® | ±ŲŅŖ²»³ä·ÖĢõ¼ž | ||
| C£® | ³äŅŖĢõ¼ž | D£® | ¼Č²»³ä·ÖŅ²²»±ŲŅŖĢõ¼ž |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\frac{1}{2}$ | B£® | $\frac{\sqrt{3}}{2}$ | C£® | $\sqrt{3}$ | D£® | $\frac{3\sqrt{13}}{26}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
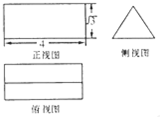 Ņ»øöÕżĄāÖł£Øµ×ĆęŹĒÕżČż½ĒŠĪ”¢²ąĄā“¹Ö±ÓŚµ×ĆęµÄĄāÖł£©µÄČżŹÓĶ¼ČēĶ¼ĖłŹ¾£¬ŌņøĆČżĄāÖłµÄ±ķĆ껿µČÓŚ£Ø””””£©
Ņ»øöÕżĄāÖł£Øµ×ĆęŹĒÕżČż½ĒŠĪ”¢²ąĄā“¹Ö±ÓŚµ×ĆęµÄĄāÖł£©µÄČżŹÓĶ¼ČēĶ¼ĖłŹ¾£¬ŌņøĆČżĄāÖłµÄ±ķĆ껿µČÓŚ£Ø””””£©| A£® | 2$\sqrt{3}$+12 | B£® | 2$\sqrt{3}$+24 | C£® | 2$\sqrt{3}$+12 | D£® | 6$\sqrt{3}$+24 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | aÓė|a|ŹĒ¼ÆŗĻAÖŠµÄĮ½øö²»Ķ¬ŌŖĖŲ | |
| B£® | ·½³Ģ£Øx-1£©2£Øx-2£©=0µÄ½ā¼ÆÓŠ3øöŌŖĖŲ | |
| C£® | Å×ĪļĻßy=x2ÉĻµÄĖłÓŠµć×é³ÉµÄ¼ÆŗĻŹĒÓŠĻŽ¼Æ | |
| D£® | ²»µČŹ½x2+1”Ü0µÄ½ā¼ÆŹĒæÕ¼Æ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 3”ŹA | B£® | 1”ŹA | C£® | 0∉A | D£® | -1”ŹA |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com