
分析 由题意和对数的真数大于零得:x∈(-∞,1]时,$\frac{1+{2}^{x}+{3}^{x}+…+9{9}^{x}+a•10{0}^{x}}{100}>0$恒成立,利用分离常数法化简,再构造函数y=-[${(\frac{1}{100})}^{x}$+${(\frac{2}{100})}^{x}$+${(\frac{3}{100})}^{x}+…+$${(\frac{99}{100})}^{x}$],利用指数函数的求出函数的值域,即可求出a的取值范围.
解答 解:由题意可得,当x∈(-∞,1]时,$\frac{1+{2}^{x}+{3}^{x}+…+9{9}^{x}+a•10{0}^{x}}{100}>0$恒成立,
则1+2x+3x+…+99x+a•100x>0恒成立,
所以a>-[${(\frac{1}{100})}^{x}$+${(\frac{2}{100})}^{x}$+${(\frac{3}{100})}^{x}+…+$${(\frac{99}{100})}^{x}$]在x∈(-∞,1]上恒成立,
因为函数y=-[${(\frac{1}{100})}^{x}$+${(\frac{2}{100})}^{x}$+${(\frac{3}{100})}^{x}+…+$${(\frac{99}{100})}^{x}$]在(-∞,1]递增,
所以y≤-($\frac{1}{100}+\frac{2}{100}+\frac{3}{100}+…+\frac{99}{100}$)=-$\frac{1+2+3+…+99}{100}$=$-\frac{99}{2}$,
则a>$-\frac{99}{2}$,
即a的取值范围是($-\frac{99}{2}$,+∞).
点评 本题考查对数、指数函数的性质,以及分离常数法、构造函数法,转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{4}$ | B. | $-\frac{{\sqrt{3}}}{4}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
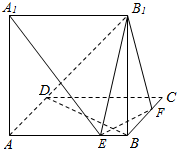 如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)
如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com