
| A. | f(sinα)>f(cosβ) | B. | f(sinα)<f(cosβ) | C. | f(sinα)>f(sinβ) | D. | f(cosα)>f(cosβ) |
分析 先判断函数f(x)的单调性,由α,β为锐角三角形的两个锐角,可得α+β>$\frac{π}{2}$,进而β>$\frac{π}{2}$-α,且β,$\frac{π}{2}$-α均为锐角,结合正弦函数的单调性和诱导公式5,可得结论.
解答  解:作出函数f(x)的图象,则函数为单调递减函数,
解:作出函数f(x)的图象,则函数为单调递减函数,
∵α,β为锐角三角形的两个锐角,
∴α+β>$\frac{π}{2}$,
∴β>$\frac{π}{2}$-α,且β,$\frac{π}{2}$-α均为锐角,
∴sinβ>sin($\frac{π}{2}$-α)=cosα,
cosβ<cos($\frac{π}{2}$-α)=sinα,
∴f(sinα)<f(cosβ),
故选:B.
点评 本题主要考查函数值的大小比较,根据数形结合判断函数的单调性,结合三角函数的诱导公式进行化简是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-2,-3) | B. | (1,-2,3) | C. | (1,2,3) | D. | (-1,2,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
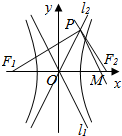 已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为( )
已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{14-2\sqrt{41}}}{2}$ | D. | $\frac{\sqrt{14+2\sqrt{41}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
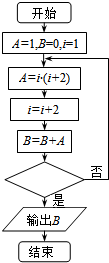 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )| A. | i≥13? | B. | i>14? | C. | i≥14? | D. | i≥15? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com