
【题目】已知函数![]() .
.
(1)若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)若在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 下方,求
下方,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用函数在![]() 处切线的斜率为
处切线的斜率为![]() 可求得
可求得![]() .将切点坐标代入切线方程可求得
.将切点坐标代入切线方程可求得![]() .(2)构造函数
.(2)构造函数![]() ,则问题转化为
,则问题转化为![]() 在区间
在区间![]() 上恒成立.对
上恒成立.对![]() 求导后,对
求导后,对![]() 分成
分成![]() 三类,讨论函数的单调区间和最值,由此求得
三类,讨论函数的单调区间和最值,由此求得![]() 的取值范围.
的取值范围.
试题解析:(1)由题知:![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
所以切点为![]() ,代入切线方程得:
,代入切线方程得:![]() ,
,
∴![]() .
.
(2)令![]() ,则
,则![]() 的定义域为
的定义域为![]() ,
,
在区间![]() 上函数
上函数![]() 的图象恒在直线
的图象恒在直线![]() 下方,
下方,
等价于![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∵![]() ,
,
令![]() ,得
,得![]() 或
或![]() ,
,
①若![]() ,则
,则![]() ,
,
∴在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]() ,
,
此时与![]() 在区间
在区间![]() 上恒成立相背,
上恒成立相背,
∴![]() 不符合题意.
不符合题意.
②若![]() 时,则
时,则![]() ,
,
∵在![]() 上有
上有![]() ,∴
,∴![]() 在区间
在区间![]() 递增,
递增,
∴![]() ,此时与
,此时与![]() 在区间
在区间![]() 上恒成立相背,
上恒成立相背,
∴![]() 不符合题意.
不符合题意.
③若![]() ,则
,则![]() ,
,
∵在区间![]() 上有
上有![]() ,则
,则![]() 在区间
在区间![]() 递减,
递减,
∴![]() 在
在![]() 恒成立,要使
恒成立,要使![]() 在
在![]() 恒成立,
恒成立,
只需![]() ,∴
,∴![]() ,
,
∴![]() .
.
综上,当![]() 时,函数
时,函数![]() 的图象恒在直线
的图象恒在直线![]() 下方.
下方.


科目:高中数学 来源: 题型:
【题目】如右图所示,设E、F、E1、F1分别是长方体ABCD-A1B1C1D1的棱AB、CD、A1B1、C1D1的中点,则平面EFD1A1与平面BCF1E1的位置关系是 ( )

A. 平行 B. 相交 C. 异面 D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
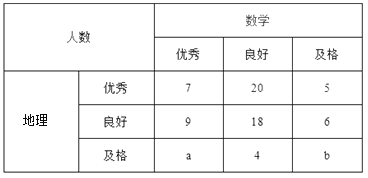
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有![]() .
.
(Ⅰ)若在该样本中,数学成绩优秀率是30%,求![]() 的值;
的值;
(Ⅱ)已知![]() ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·桂林高二检测)如图所示,在四边形ABCD中,AB=AD=CD=1,BD=![]() ,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.
,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是________.

(1)A′C⊥BD.(2)∠BA′C=90°.
(3)CA′与平面A′BD所成的角为30°.
(4)四面体A′-BCD的体积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com