
分析 直线ax+by+2b-a=0化为a(x-1)+b(y+2)=0,令$\left\{\begin{array}{l}{x-1=0}\\{y+2=0}\end{array}\right.$,可得直线ax+by+2b-a=0过定点Q(1,-2).可知:垂足N在以MQ为直径的圆上,圆心即相等MQ的中点C(0,-1).|PN|的最大值为|PC|+r.
解答 解:直线ax+by+2b-a=0化为a(x-1)+b(y+2)=0,令$\left\{\begin{array}{l}{x-1=0}\\{y+2=0}\end{array}\right.$,解得x=1,y=-2.
∴直线ax+by+2b-a=0过定点Q(1,-2).
∴垂足N在以MQ为直径的圆上,
圆心即相等MQ的中点C(0,-1).
其圆的方程为:x2+(y+1)2=2.
|PC|=$\sqrt{5}$.
∴|PN|的最大值为$\sqrt{5}+\sqrt{2}$.
故答案为:$\sqrt{5}+\sqrt{2}$.
点评 本题考查了直线与圆的方程、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\widehat{y}$=5-17x | B. | $\widehat{y}$=-17+5x | C. | $\widehat{y}$=17+5x | D. | $\widehat{y}$=17-5x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知△ABC满足∠B>∠C,∠A的平分线和过顶点的高线、中线与边BC分别交与点L、H、D.证明∠HAL=∠DAL的充分必要条件是∠BAC=90°.
已知△ABC满足∠B>∠C,∠A的平分线和过顶点的高线、中线与边BC分别交与点L、H、D.证明∠HAL=∠DAL的充分必要条件是∠BAC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
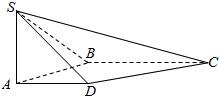 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=$\sqrt{n}$-$\sqrt{n-1}$ | B. | an=$\sqrt{n}$+$\sqrt{n-1}$ | C. | an=$\sqrt{n}$-$\sqrt{n+1}$ | D. | an=$\sqrt{n}$+$\sqrt{n+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
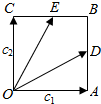 如图所示,四边形OABC是边长为1的正方形,$\overrightarrow{OA}$=e1,$\overrightarrow{OC}$=e2,D、E分别为AB、BC中点.
如图所示,四边形OABC是边长为1的正方形,$\overrightarrow{OA}$=e1,$\overrightarrow{OC}$=e2,D、E分别为AB、BC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com