
【题目】已知点![]()
![]() ,圆
,圆![]() :
: ![]() ,过
,过![]() 的动直线
的动直线![]() 与⊙
与⊙![]() 交
交![]() 两点,线段
两点,线段![]() 中点为
中点为![]() ,
, ![]() 为坐标原点。
为坐标原点。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程以及△
的方程以及△![]() 面积。
面积。
【答案】(Ⅰ)![]() (Ⅱ)直线
(Ⅱ)直线![]() 的方程为3x-y-8=0,△
的方程为3x-y-8=0,△![]() 面积是
面积是![]()
【解析】试题分析:(Ⅰ)圆C的方程可化为(x-4)2+y2=16,由此能求出圆心为C(4,0),半径为4,设M(x,y),求出向量CM,MP的坐标,由![]() 运用向量的数量积的坐标表示,化简整理求出M的轨迹方程;
运用向量的数量积的坐标表示,化简整理求出M的轨迹方程;
(Ⅱ)由(Ⅰ)知M的轨迹是以点N(3,-1)为圆心, ![]() 为半径的圆.由于|OP|=|OM|,故O在线段PM的垂直平分线上,可得ON⊥PM,由直线垂直的条件:斜率之积为-1,再由点斜式方程可得直线l的方程.利用点到直线距离公式结合已知条件能求出△POM的面积
为半径的圆.由于|OP|=|OM|,故O在线段PM的垂直平分线上,可得ON⊥PM,由直线垂直的条件:斜率之积为-1,再由点斜式方程可得直线l的方程.利用点到直线距离公式结合已知条件能求出△POM的面积
试题解析:
(Ⅰ)圆C的方程可化为: ![]() ,所以圆心C(4,0)半径为4。
,所以圆心C(4,0)半径为4。
设M(x,y),则![]() (x-4,y),
(x-4,y),![]() 则由条件知,
则由条件知, ![]()
故(x-4)(2-x)+y(2-y)=0,即![]() 。由于点P在圆C的内部,所以M的轨迹方程是
。由于点P在圆C的内部,所以M的轨迹方程是![]() 。
。
(Ⅱ)由(Ⅰ)可知M的轨迹是以点N(3,-1)为圆心,以![]() 为半径的圆。又
为半径的圆。又![]() ,故O在线段PM的垂直平分线上,显然P在圆N上,从而ON⊥PM。KON=
,故O在线段PM的垂直平分线上,显然P在圆N上,从而ON⊥PM。KON=![]() ,所以直线
,所以直线![]() 的斜率为3,故直线
的斜率为3,故直线![]() 的方程为3x-y-8=0.又
的方程为3x-y-8=0.又![]() =
=![]() ,O到
,O到![]() 的距离为
的距离为![]() ,由勾股定理可得|PM|=
,由勾股定理可得|PM|=![]() ,所以△
,所以△![]() 面积是
面积是![]() 。
。


科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2016年11月份人均用电情况进行统计后,按人均用电量分为
位居民2016年11月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
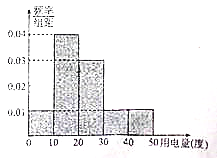
A. 11月份人均用电量人数最多的一组有![]() 人
人
B. 11月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. 11月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的中心在原点,焦点在x轴,焦距为2,且长轴长是短轴长的![]() 倍.
倍.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)设P(2,0),过椭圆E左焦点F的直线l交E于A、B两点,若对满足条件的任意直线l,不等式![]() ≤λ(λ∈R)恒成立,求λ的最小值.
≤λ(λ∈R)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() (
(![]() ,
, ![]() 为常数).
为常数).
(1)判断曲线![]() 的形状;
的形状;
(2)设曲线![]() 分别与
分别与![]() 轴,
轴, ![]() 轴交于点
轴交于点![]() ,
, ![]() (
(![]() ,
, ![]() 不同于原点
不同于原点![]() ),试判断
),试判断![]() 的面积
的面积![]() 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;
(3)设直线![]() :
: ![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩阵![]() 将直线l:x+y-1=0变换成直线l′.
将直线l:x+y-1=0变换成直线l′.
(1)求直线l′的方程;
(2)判断矩阵A是否可逆?若可逆,求出矩阵A的逆矩阵A-1;若不可逆,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com