
ЎҫМвДҝЎҝДіі§ПъКЫІҝТФПдОӘөҘО»ПъКЫДіЦЦБгјюЈ¬ГҝПдөД¶ЁјЫОӘ![]() ФӘЈ¬өНУЪ
ФӘЈ¬өНУЪ![]() Пд°ҙФӯјЫПъКЫЈ¬І»өНУЪ
Пд°ҙФӯјЫПъКЫЈ¬І»өНУЪ![]() ПдФтУРТФПВБҪЦЦУЕ»Э·Ҫ°ёЈәўЩТФ
ПдФтУРТФПВБҪЦЦУЕ»Э·Ҫ°ёЈәўЩТФ![]() ПдОӘ»щЧјЈ¬Гҝ¶а
ПдОӘ»щЧјЈ¬Гҝ¶а![]() ПдЛН
ПдЛН![]() ПдЈ»ўЪНЁ№эЛ«·ҪТйјЫЈ¬Вт·ҪДЬТФУЕ»Э
ПдЈ»ўЪНЁ№эЛ«·ҪТйјЫЈ¬Вт·ҪДЬТФУЕ»Э![]() іЙҪ»өДёЕВКОӘ
іЙҪ»өДёЕВКОӘ![]() Ј¬ТФУЕ»Э
Ј¬ТФУЕ»Э![]() іЙҪ»өДёЕВКОӘ
іЙҪ»өДёЕВКОӘ![]() .
.
![]() јЧЎўТТБҪөҘО»¶јТӘФЪёГі§№әВт
јЧЎўТТБҪөҘО»¶јТӘФЪёГі§№әВт![]() ПдХвЦЦБгјюЈ¬БҪөҘО»¶јСЎФс·Ҫ°ёўЪЈ¬ЗТёчЧФҙпіЙөДіЙҪ»јЫёсПа»Ҙ¶АБўЈ¬ЗујЧөҘО»УЕ»ЭұИАэІ»өНУЪТТөҘО»УЕ»ЭұИАэөДёЕВКЈ»
ПдХвЦЦБгјюЈ¬БҪөҘО»¶јСЎФс·Ҫ°ёўЪЈ¬ЗТёчЧФҙпіЙөДіЙҪ»јЫёсПа»Ҙ¶АБўЈ¬ЗујЧөҘО»УЕ»ЭұИАэІ»өНУЪТТөҘО»УЕ»ЭұИАэөДёЕВКЈ»
![]() ДіөҘО»РиТӘХвЦЦБгјю
ДіөҘО»РиТӘХвЦЦБгјю![]() ПдЈ¬ТФ№әВтЧЬјЫөДКэС§ЖЪНыОӘҫцІЯТАҫЭЈ¬КФОКёГөҘО»СЎФсДДЦЦУЕ»Э·Ҫ°ёёь»®ЛгЈҝ
ПдЈ¬ТФ№әВтЧЬјЫөДКэС§ЖЪНыОӘҫцІЯТАҫЭЈ¬КФОКёГөҘО»СЎФсДДЦЦУЕ»Э·Ҫ°ёёь»®ЛгЈҝ
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©СЎФс·Ҫ°ёўЩёь»®ЛгЈ®
Ј»ЈЁ2Ј©СЎФс·Ҫ°ёўЩёь»®ЛгЈ®
ЎҫҪвОцЎҝ
ЈЁ1Ј©АыУГ¶ФБўКВјюёЕВК№«КҪјҙҝЙөГөҪҪб№ыЈ»
ЈЁ2Ј©ЙиФЪХЫҝЫУЕ»ЭЦРГҝПдБгјюөДјЫёсОӘXФӘЈ¬ФтXЈҪ184»т188Ј®өГөҪПаУҰөД·ЦІјБРј°ЖЪНыЦөЈ¬јЖЛгБҪЦЦ·Ҫ°ё№әВтЧЬјЫөДКэС§ЖЪНыҙУ¶шЧчіцЕР¶П.
(1)ТтОӘјЧөҘО»УЕ»ЭұИАэөНУЪТТөҘО»УЕ»ЭұИАэөДёЕВКОӘ0.4ЎБ0.6=0.24Ј¬
ЛщТФјЧөҘО»УЕ»ЭұИАэІ»өНУЪТТөҘО»УЕ»ЭұИАэөДёЕВК1-0.24=0.76Ј®
(2)ЙиФЪХЫҝЫУЕ»ЭЦРГҝПдБгјюөДјЫёсОӘXФӘЈ¬ФтXЈҪ184»т188Ј®
XөД·ЦІјБРОӘ
X | 184 | 188 |
P | 0.6 | 0.4 |
ФтEXЈҪ184ЎБ0.6+188ЎБ0.4ЈҪ185.6Ј®
ИфСЎФс·Ҫ°ёўЪЈ¬Фт№әВтЧЬјЫөДКэС§ЖЪНыОӘ185.6ЎБ650ЈҪ120640ФӘЈ®
ИфСЎФс·Ҫ°ёўЩЈ¬УЙУЪ№әВт600ПдДЬ»сФщ50ПдЈ¬ЛщТФёГөҘО»Ц»РиТӘ№әВт600ПдЈ¬
ҙУ¶ш№әВтЧЬјЫОӘ200ЎБ600ЈҪ120000ФӘЈ®
ТтОӘ120640>120000Ј¬ЛщТФСЎФс·Ҫ°ёўЩёь»®ЛгЈ®
ЖА·ЦПёФтЈә
өЪ(1)ОКЦРЈ¬·ЦИэЦЦЗйҝцЗуёЕВКЈ¬јҙЛщЗуёЕВКОӘ0.6ЎБ0.4+0.42+0.62ЈҪ0.76Н¬СщөГ·ЦЈ»
өЪ(2)ОКЦРЈ¬ФЪ·Ҫ°ёўЪЦұҪУјЖЛг№әВтЧЬјЫөДКэС§ЖЪНыТІКЗҝЙТФөДЈ¬ҪвОц№эіМЧчИзПВПаУҰөДөчХыЈә
ЙиФЪХЫҝЫУЕ»ЭЦР№әВтЧЬјЫОӘXФӘЈ¬ФтXЈҪ184ЎБ650»т188ЎБ650Ј®
XөД·ЦІјБРОӘ
X | 184ЎБ650 | 188ЎБ650 |
P | 0.6 | 0.4 |
ФтEXЈҪ184ЎБ650ЎБ0.6+188ЎБ650ЎБ0.4ЈҪ120640Ј®


 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() өДУТҪ№өгОӘ
өДУТҪ№өгОӘ![]() Ј¬
Ј¬![]() ОӘ¶МЦбөДТ»ёц¶ЛөгЗТ
ОӘ¶МЦбөДТ»ёц¶ЛөгЗТ![]() ЈЁЖдЦР
ЈЁЖдЦР![]() ОӘЧшұкФӯөгЈ©.
ОӘЧшұкФӯөгЈ©.
ЈЁ1Ј©ЗуНЦФІөД·ҪіМ;
ЈЁ2Ј©Иф![]() Ўў
Ўў![]() ·ЦұрКЗНЦФІіӨЦбөДЧуУТ¶ЛөгЈ¬¶Ҝөг
·ЦұрКЗНЦФІіӨЦбөДЧуУТ¶ЛөгЈ¬¶Ҝөг![]() ВъЧг
ВъЧг![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]() Ј¬Ҫ»НЦФІУЪөг
Ј¬Ҫ»НЦФІУЪөг![]() Ј¬КФОК
Ј¬КФОК![]() ЦбЙПКЗ·сҙжФЪТмУЪөг
ЦбЙПКЗ·сҙжФЪТмУЪөг![]() өД¶Ёөг
өД¶Ёөг![]() Ј¬К№өГТФ
Ј¬К№өГТФ![]() ОӘЦұҫ¶өДФІәг№эЦұПЯ
ОӘЦұҫ¶өДФІәг№эЦұПЯ![]() Ўў
Ўў![]() өДҪ»өгЈ¬ИфҙжФЪЈ¬Зуіцөг
өДҪ»өгЈ¬ИфҙжФЪЈ¬Зуіцөг![]() өДЧшұкЈ»ИфІ»ҙжФЪ,ЛөГчАнУЙ.
өДЧшұкЈ»ИфІ»ҙжФЪ,ЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬![]() ЗТ
ЗТ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ЗТ
ЗТ![]() Ј¬
Ј¬![]() ЗТ
ЗТ![]() Ј¬
Ј¬![]() ЖҪГж
ЖҪГж![]() Ј¬
Ј¬![]() .
.
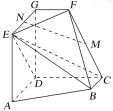
ЈЁ1Ј©Иф![]() ОӘ
ОӘ![]() өДЦРөгЈ¬
өДЦРөгЈ¬![]() ОӘ
ОӘ![]() өДЦРөгЈ¬ЗуЦӨЈә
өДЦРөгЈ¬ЗуЦӨЈә![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©Зу¶юГжҪЗ![]() өДХэПТЦөЈ®
өДХэПТЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ¶ҜФІ![]() ФЪФІ
ФЪФІ![]() Јә
Јә![]() НвІҝЗТУлФІ
НвІҝЗТУлФІ![]() ПаЗРЈ¬Н¬Кұ»№ФЪФІ
ПаЗРЈ¬Н¬Кұ»№ФЪФІ![]() Јә
Јә![]() ДЪІҝУлФІ
ДЪІҝУлФІ![]() ПаЗРЈ®
ПаЗРЈ®
ЈЁ1Ј©Зу¶ҜФІФІРД![]() өД№мјЈ·ҪіМЈ»
өД№мјЈ·ҪіМЈ»
ЈЁ2Ј©јЗЈЁ1Ј©ЦРЗуіцөД№мјЈОӘ![]() Ј¬
Ј¬![]() Ул
Ул![]() ЦбөДБҪёцҪ»өг·ЦұрОӘ
ЦбөДБҪёцҪ»өг·ЦұрОӘ![]() Ўў
Ўў![]() Ј¬
Ј¬![]() КЗ
КЗ![]() ЙПТмУЪ
ЙПТмУЪ![]() Ўў
Ўў![]() өД¶ҜөгЈ¬УЦЦұПЯ
өД¶ҜөгЈ¬УЦЦұПЯ![]() Ул
Ул![]() ЦбҪ»УЪөг
ЦбҪ»УЪөг![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() Ўў
Ўў![]() ·ЦұрҪ»ЦұПЯ
·ЦұрҪ»ЦұПЯ![]() УЪ
УЪ![]() Ўў
Ўў![]() БҪөгЈ¬ЗуЦӨЈә
БҪөгЈ¬ЗуЦӨЈә![]() ОӘ¶ЁЦөЈ®
ОӘ¶ЁЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ·ЗБгПтБҝБР![]() ВъЧгЈә
ВъЧгЈә![]() Ј¬
Ј¬![]() Ј¬ЈЁ
Ј¬ЈЁ![]() Ј¬
Ј¬![]() Ј©.
Ј©.
ЈЁ1Ј©ЦӨГчЈәКэБР![]() КЗөИұИКэБРЈ»
КЗөИұИКэБРЈ»
ЈЁ2Ј©ПтБҝ![]() Ул
Ул![]() өДјРҪЗЈ»
өДјРҪЗЈ»
ЈЁ3Ј©Йи![]() Ј¬Ҫ«
Ј¬Ҫ«![]() ЦРЛщУРУл
ЦРЛщУРУл![]() №ІПЯөДПтБҝ°ҙФӯАҙөДЛіРтЕЕіЙТ»БРЈ¬јЗЧч
№ІПЯөДПтБҝ°ҙФӯАҙөДЛіРтЕЕіЙТ»БРЈ¬јЗЧч![]() Ј¬Бо
Ј¬Бо![]() Ј¬
Ј¬![]() ОӘЧшұкФӯөгЈ¬Зуөг
ОӘЧшұкФӯөгЈ¬Зуөг![]() өДЧшұк.
өДЧшұк.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЛИӨРЎЧйУРДРЙъ20ИЛЈ¬Е®Йъ10ИЛЈ¬ҙУЦРійИЎТ»ёцИЭБҝОӘ5өДСщұҫЈ¬ЗЎәГійөҪ2ГыДРЙъәН3ГыЕ®ЙъЈ¬Фт
ўЩёГійСщҝЙДЬКЗПөНіійСщЈ»
ўЪёГійСщҝЙДЬКЗЛж»ъійСщЈә
ўЫёГійСщТ»¶ЁІ»КЗ·ЦІгійСщЈ»
ўЬұҫҙОійСщЦРГҝёцИЛұ»ійөҪөДёЕВК¶јКЗ![]() Ј®
Ј®
ЖдЦРЛө·ЁХэИ·өДОӘЈЁ Ј©
A.ўЩўЪўЫB.ўЪўЫC.ўЪўЫўЬD.ўЫўЬ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() өДБҪёцҪ№өгЧшұк·ЦұрКЗ
өДБҪёцҪ№өгЧшұк·ЦұрКЗ![]() Ўў
Ўў![]() Ј¬ІўЗТҫӯ№эөг
Ј¬ІўЗТҫӯ№эөг![]() .
.
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ИфЦұПЯ![]() УлФІ
УлФІ![]() Јә
Јә![]() ПаЗРЈ¬ІўУлНЦФІ
ПаЗРЈ¬ІўУлНЦФІ![]() Ҫ»УЪІ»Н¬өДБҪөг
Ҫ»УЪІ»Н¬өДБҪөг![]() Ўў
Ўў![]() .өұ
.өұ![]() Ј¬ЗТВъЧг
Ј¬ЗТВъЧг![]() КұЈ¬Зу
КұЈ¬Зу![]() Гж»э
Гж»э![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ2019Дк1ФВ1ИХЈ¬јГДП№мөАҪ»НЁ![]() әЕПЯКФФЛРРЈ¬јГДП№мөАҪ»НЁјҜНЕГжПт№гҙуКРГсҝӘХ№Ў°ІО№ЫМеСйЈ¬ХчЗуТвјыЎұ»о¶ҜЈ¬КРГсҝЙТФНЁ№эјГДПөШМъAPPЗАЖұЈ¬РЎіВЗАөҪБЛИэХЕМеСйЖұЈ¬ЧјұёҙУЛДО»ЕуУСРЎНхЈ¬РЎХЕЈ¬РЎБхЈ¬РЎАоЦРЛж»ъСЎФсБҪО»УлЧФјәТ»ЖрИҘІОјУМеСй»о¶ҜЈ¬ФтРЎНхұ»СЎЦРөДёЕВКОӘЈЁ Ј©
әЕПЯКФФЛРРЈ¬јГДП№мөАҪ»НЁјҜНЕГжПт№гҙуКРГсҝӘХ№Ў°ІО№ЫМеСйЈ¬ХчЗуТвјыЎұ»о¶ҜЈ¬КРГсҝЙТФНЁ№эјГДПөШМъAPPЗАЖұЈ¬РЎіВЗАөҪБЛИэХЕМеСйЖұЈ¬ЧјұёҙУЛДО»ЕуУСРЎНхЈ¬РЎХЕЈ¬РЎБхЈ¬РЎАоЦРЛж»ъСЎФсБҪО»УлЧФјәТ»ЖрИҘІОјУМеСй»о¶ҜЈ¬ФтРЎНхұ»СЎЦРөДёЕВКОӘЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦұПЯyЈҪ2x©ҒmУлЕЧОпПЯCЈәy2ЈҪ2pxЈЁpЈҫ0Ј©Ҫ»УЪөгAЈ¬BЈ®
ЈЁ1Ј©mЈҪpЗТ|AB|ЈҪ5Ј¬ЗуЕЧОпПЯCөД·ҪіМЈ»
ЈЁ2Ј©ИфmЈҪ4pЈ¬ЗуЦӨЈәOAЎНOBЈЁOОӘЧшұкФӯөгЈ©Ј®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com