
【题目】已知函数![]() 。
。
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 的最大值
的最大值![]() ,
,![]() 存在最小值
存在最小值![]() ,且
,且![]() ,求证:
,求证:![]() 。
。
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,![]() 在
在![]() 单调递减;(2)证明见解析。
单调递减;(2)证明见解析。
【解析】
试题分析:(1)先求![]() ,讨论
,讨论![]() 和
和![]() 两种情况,分别令
两种情况,分别令![]() 得减区间,
得减区间,![]() 得增区间;(2)由(1)可知
得增区间;(2)由(1)可知![]() ,且
,且![]() ,(
,(![]() 为
为![]() 的极值点),由题设
的极值点),由题设![]() ,即
,即![]() ,将
,将![]() 代入上式,得
代入上式,得![]() ,则
,则![]() 。
。
试题解析:(1)由题设有![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,列表如下:
时,列表如下:
|
|
|
|
|
| 0 |
|
| 递增 | 最大值 | 递减 |
可知,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
(2)由题设有![]() ,
,
若![]() ,
,![]() 在其定义域
在其定义域![]() 上单调递增,无最小值,由(1)可知此时
上单调递增,无最小值,由(1)可知此时![]() 无最大值,故而
无最大值,故而![]() 令
令![]() ,又
,又![]() ,
,
故唯一存在![]() ,使得
,使得![]() ,即
,即![]() ,
,
列表如下
|
|
|
|
|
| 0 |
|
|
| 0 |
|
| 递减 | 最小值 | 递增 |
由(1)可知![]() ,且
,且![]() ,由题设
,由题设![]() ,即
,即![]() ,将
,将![]() 代入上式有
代入上式有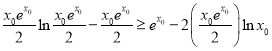 ,化简得
,化简得![]() 。构造函数
。构造函数![]() ,
,
![]() ,易知
,易知![]() 为单调递增函数,又
为单调递增函数,又![]() ,而当
,而当![]() ,则唯一存在
,则唯一存在![]() ,使得
,使得![]() ,则当
,则当![]() 递减,当
递减,当![]() ,
,![]() ,
,![]() 递增。又
递增。又![]() ,故
,故![]() 只会在
只会在![]() 有解,而
有解,而![]() ,故(*)的解为
,故(*)的解为![]() ,则
,则![]() 。
。


科目:高中数学 来源: 题型:
【题目】如下图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米。

(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月15日,天宫二号实验室发射成功.借天宫二号东风,某厂推出品牌为“玉兔”的新产品.生产“玉兔”的固定成本为20000元,每生产一件“玉兔”需要增加投入100元.根据初步测算,总收益(单位:元)满足分段函数![]() ,其中
,其中 ,
,![]() 是“玉兔”的月产量(单位:件),总收益=总成本+利润.
是“玉兔”的月产量(单位:件),总收益=总成本+利润.
(I)试将利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(II)当月产量为多少件时利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)是否存在![]() 及过原点的直线
及过原点的直线![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() ,
,![]() 均相切?若存在,求
均相切?若存在,求![]() 的值及直线
的值及直线![]() 的方程;若不存在,请说明理由;
的方程;若不存在,请说明理由;
(2)若函数![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了规定学校办学,省电教育厅督察组对某所高中进行了抽样调查,抽查到班级一共有52名学生,现将该班学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知7号,33号,46号同学在样本中,那么样本中还有一位同学的编号应是( )
A.13
B.19
C.20
D.52
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com