
�����ĵ���Ϊ0�ĵ��Ϊ������פ�㣬����(1,1)Ϊ����f(x)��פ�㣬���f(x)���С�1—1פ���ԡ�.
��1���躯��f(x)=-x+2![]() +alnx������a��0��
+alnx������a��0��
����֤������f(x)�����С�1—1פ���ԡ���������f(x)�ĵ�������
��2����֪����g(x)=bx3+3x2+cx+2���С�1—1פ���ԡ�������x1��x2ÎR��x1��x2�����Ϊʵ�����Ҧˡ�-1����=![]() ����=
����=![]() ����|g(��)-g(��)|��|g(x1)-g(x2)|����˵�ȡֵ��Χ.
����|g(��)-g(��)|��|g(x1)-g(x2)|����˵�ȡֵ��Χ.
�⣺����![]() =-1+
=-1+![]() +
+![]() ��
��![]() =-1+1+a��0��
=-1+1+a��0��
�ຯ��f(x)�����С�1—1פ���ԡ�.��������������������������������2��
����![]() =
=![]() =
= 
(ⅰ)��a+![]() ��0,��a��-
��0,��a��-![]() ʱ��
ʱ��![]() ��0.��f(x)��(0,+��)�ϵļ�������
��0.��f(x)��(0,+��)�ϵļ�������
(ⅱ)��a+![]() =0,��a=-
=0,��a=-![]() ʱ����Ȼ
ʱ����Ȼ![]() ��0.��f(x)��(0,+��)�ϵļ�������������������������������4��
��0.��f(x)��(0,+��)�ϵļ�������������������������������4��
(ⅲ)��a+![]() ��0����a��-
��0����a��-![]() ʱ����
ʱ����![]() =0��
=0��![]() =
=![]() ��
��![]() ��������������������������������6��
��������������������������������6��
��-![]() ��a��0ʱ��
��a��0ʱ��![]() -
-![]() ��0��xÎ(0, a+
��0��xÎ(0, a+![]() -
-![]() )ʱ��
)ʱ��![]() ��0;
��0;
xÎ( a+![]() -
-![]() , a+
, a+![]() +
+![]() )ʱ��
)ʱ��![]() ��0; xÎ( a+
��0; xÎ( a+![]() +
+![]() , +��)ʱ��
, +��)ʱ��![]() ��0;
��0;
��a��0ʱ��![]() -
-![]() ��0 ��xÎ(0, a+
��0 ��xÎ(0, a+![]() +
+![]() )ʱ��
)ʱ��![]() ��0; xÎ( a+
��0; xÎ( a+![]() +
+![]() ,+��)ʱ��
,+��)ʱ��![]() ��0;
��0;
������������a��-![]() ʱ������f(x)�ĵ����ݼ�����Ϊ(0,+��)��
ʱ������f(x)�ĵ����ݼ�����Ϊ(0,+��)��
��-![]() ��a��0ʱ������f(x)�ĵ����ݼ�����Ϊ(0, a+
��a��0ʱ������f(x)�ĵ����ݼ�����Ϊ(0, a+![]() -
-![]() )��( a+
)��( a+![]() +
+![]() ,+��)��
,+��)��
����f(x)�ĵ�����������Ϊ( a+![]() -
-![]() , a+
, a+![]() +
+![]() )��
)��
��a��0ʱ,����f(x)�ĵ�����������Ϊ(0, a+![]() +
+![]() )��
)��
����f(x)�ĵ����ݼ�����Ϊ( a+![]() +
+![]() , +��)����������������������������������9��
, +��)����������������������������������9��
����������ã�![]() =3bx2+6x+c,��g(x)���С�1—1פ���ԡ���
=3bx2+6x+c,��g(x)���С�1—1פ���ԡ���![]() ��
��![]()
��![]() ���
���![]() ��
��![]() =-3x2+6x-3=-3(x-1)2��0����g(x)�ڶ�����R�ϵ����ݼ�.
=-3x2+6x-3=-3(x-1)2��0����g(x)�ڶ�����R�ϵ����ݼ�.
�ٵ��ˡ�0ʱ���Ц�=![]() ��
��![]() =x1����=
=x1����=![]() ��
��![]() =x2������Î[x1,x2),ͬ����Î(x1,x2] ������11��
=x2������Î[x1,x2),ͬ����Î(x1,x2] ������11��
��g(x)�ĵ����Կ�֪��g(��)��g(��)Î[ g(x2),g(x1)]��|g(��)-g(��)|��|g(x1)-g(x2)|������|g(��)-g(��)|��|g(x1)-g(x2)|����.
�ڵ�-1���ˣ�0ʱ����=![]() ��
��![]() =x1����=
=x1����=![]() ��
��![]() =x2����������������������������13��
=x2����������������������������13��
������x1��x2���¡�g(��)��g(x2)��g(x1)��g(��)��|g(��)-g(��)|��|g(x1)-g(x2)|����������
�۵��ˣ�-1ʱ����=![]() ��
��![]() =x2, ��=
=x2, ��=![]() ��
��![]() =x1�����£�x1��x2����
=x1�����£�x1��x2����
��g(��)��g(x2)��g(x1)��g(��)��|g(��)-g(��)|��|g(x1)-g(x2)|Ҳ�������衭���� ����������������15��
�ɴˣ��ۺϢ٢ڢ۵�����Ħ˵�ȡֵ��Χ�Ǧˣ�0�Ҧˡ�-1



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x |
| x1+��x2 |
| 1+�� |
| x2+��x1 |
| 1+�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 +alnx������a��0��
+alnx������a��0��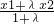 ����=
����=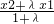 ����|g������-g���£�|��|g��x1��-g��x2��|����˵�ȡֵ��Χ��
����|g������-g���£�|��|g��x1��-g��x2��|����˵�ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ�����и߿���ѧģ���Ծ���3���������棩 ���ͣ������
 +alnx������a��0��
+alnx������a��0�� ����=
����= ����|g������-g���£�|��|g��x1��-g��x2��|����˵�ȡֵ��Χ��
����|g������-g���£�|��|g��x1��-g��x2��|����˵�ȡֵ��Χ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com