
【题目】已知函数![]() 满足
满足![]() ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,则实数
恰有4个不同的实数解,则实数![]() 的取值范围是___________.
的取值范围是___________.
【答案】![]()
【解析】
由题意,把在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,转化为函数
恰有4个不同的实数解,转化为函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有4个不同的交点,作出函数的图象,结合图象,分类讨论,即可求解,得到答案.
内有4个不同的交点,作出函数的图象,结合图象,分类讨论,即可求解,得到答案.
由题意,函数![]() 满足
满足![]() ,即
,即![]() ,即函数
,即函数![]() 是以6为周期的周期函数,
是以6为周期的周期函数,
又由在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,
恰有4个不同的实数解,
即在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,
恰有4个不同的实数解,
即函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有4个不同的交点,
内有4个不同的交点,
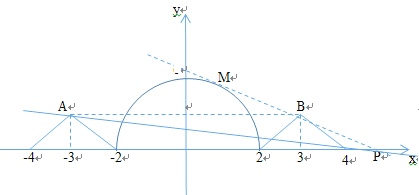
又由函数![]() ,作出函数的图象,如图所示,
,作出函数的图象,如图所示,
由直线![]() ,可知直线恒过点
,可知直线恒过点![]() ,
,
当![]() 时,此时直线
时,此时直线![]() 与函数
与函数![]() 的图象恰有4个交点,
的图象恰有4个交点,
当直线过点![]() 时,此时
时,此时![]() ,即
,即![]() ,此时函数
,此时函数![]() 与直线
与直线![]() 有5个同的交点,
有5个同的交点,
当直线![]() 与半圆
与半圆![]() 相切时,此时圆心到直线
相切时,此时圆心到直线![]() 的距离等于圆的半径,即
的距离等于圆的半径,即![]() ,解得
,解得![]() 或
或![]() (舍去),此时函数
(舍去),此时函数![]() 与直线
与直线![]() 有3个同的交点,
有3个同的交点,
此时函数![]() 与直线
与直线![]() 恰有4个同的交点,则
恰有4个同的交点,则![]()
综上可知,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学图书馆举行高中志愿者检索图书的比赛,从高一、高二两个年级各抽取10名志愿者参赛。在规定时间内,他们检索到的图书册数的茎叶图如图所示,规定册数不小于20的为优秀.
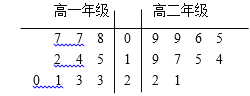
(Ⅰ) 从两个年级的参赛志愿者中各抽取两人,求抽取的4人中至少一人优秀的概率;
(Ⅱ) 从高一10名志愿者中抽取一人,高二10名志愿者中抽取两人,3人中优秀人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于概率和统计的几种说法:①10名工人某天生产同一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为![]() ,中位数为
,中位数为![]() ,众数为
,众数为![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系为
的大小关系为![]() ;②样本4,2,1,0,-2的标准差是2;③在面积为
;②样本4,2,1,0,-2的标准差是2;③在面积为![]() 的
的![]() 内任选一点
内任选一点![]() ,则随机事件“
,则随机事件“![]() 的面积小于
的面积小于![]() ”的概率为
”的概率为![]() ;④从写有0,1,2,…,9的十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片上的数字各不相同的概率是
;④从写有0,1,2,…,9的十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片上的数字各不相同的概率是![]() .其中正确说法的序号有______.
.其中正确说法的序号有______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
科目:高中数学 来源: 题型:
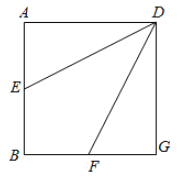
【题目】如图,棱长为![]() 的正方形
的正方形![]() 中,点
中,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,将
,将![]() ,
,![]() 沿
沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 两点重合于
两点重合于![]() 点上,设
点上,设![]() 与
与![]() 交于
交于![]() 点,过点
点,过点![]() 作
作![]() 于
于![]() 点.
点.
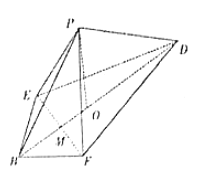
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() (不过坐标原点)与椭圆
(不过坐标原点)与椭圆![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上方,点
轴上方,点![]() 在
在![]() 轴下方,若
轴下方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com