练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】将A，B两枚骰子各抛掷一次，观察向上的点数，问：
    （1）共有多少种不同的结果？
    （2）两枚骰子点数之和是3的倍数的结果有多少种？
    （3）两枚骰子点数之和是3的倍数的概率为多少？

    【答案】
    （1）解：第一枚有6种结果，

    第二枚有6种结果，由分步计数原理知共有6×6=36种结果


    （2）解：可以列举出两枚骰子点数之和是3的倍数的结果（1，2）（1，5）（2，1）（2，4）（3，3）（3，6）（4，2）（4，5）（5，1）（5，4）（6，3）（6，6）共有12种结果．
    （3）解：本题是一个古典概型

    由上两问知试验发生包含的事件数是36，

    满足条件的事件数是12，

    ∴根据古典概型概率公式得到P= =


    【解析】（1）已知第一枚由6种结果，第二枚有6种结果，根据分步计数乘法原理，把两次的结果数相乘，得到共有的结果数．（2）比值两个有序数对中第一个数字作为第一枚的结果，把第二个数字作为第二枚的结果，列举出所有满足题意的结果．（3）本题是一个古典概型由上两问知试验发生包含的事件数是36，满足条件的事件数是12，根据古典概型的概率公式，做出要求的概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|2x﹣a|+a．
    （1）当a=2时，求不等式f（x）≤6的解集；
    （2）设函数g（x）=|2x﹣1|，当x∈R时，f（x）+g（x）≥3，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数
    （1）求函数f（x）的对称中心和函数的单调递增区间；
    （2）已知△ABC中，角A，B，C的对边分别为a，b，c，若 ，求AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=sinx的图象向右平移三个单位长度得到图象C，再将图象C上的所有点的横坐标变为原来的倍（纵坐标不变）得到图象C1 ， 则C1的函数解析式为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，∠C= ，AC=BC，M、N分别是BC、AB的中点，将△BMN沿直线MN折起，使二面角B′﹣MN﹣B的大小为 ，则B'N与平面ABC所成角的正切值是（ ）

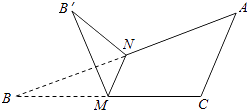
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥 的底面为正方形， ⊥底面 ，则下列结论中不正确的是（ ）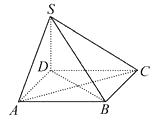

    A.
    B. ∥平面
    C. 与 所成的角等于 与 所成的角
    D. 与平面 所成的角等于 与平面 所成的角

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长都相等的四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，则下面四个结论中不成立的是 ( )
    A.BC∥平面PDF
    B.DF⊥平面PAE
    C.平面PDF⊥平面ABC
    D.平面PAE⊥平面ABC

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱锥P﹣ABC中，D，E分别是BC，AC的中点．PB=PC=AB=2，AC=4，BC=2 ，PA= ．

    （1）求证：平面ABC⊥平面PED；
    （2）求AC与平面PBC所成的角；
    （3）求平面PED与平面PAB所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂修建一个长方体形无盖蓄水池，其容积为4800立方米，深度为3米．池底每平方米的造价为150元，池壁每平方米的造价为120元．设池底长方形长为x米．
    （Ⅰ）求底面积并用含x的表达式表示池壁面积；
    （Ⅱ）怎样设计水池能使总造价最低？最低造价是多少？

    查看答案和解析>>

    同步练习册答案