练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，直线的参数方程为为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （1）求直线的普通方程与曲线的直角坐标方程；

    （2）若直线与曲线交于，两点，且设定点，求的值．

    【答案】（1）的普通方程为；曲线的直角坐标方程为：．（2）

    【解析】

    （1）由直线的参数方程，消去参数，即可求得直线的普通方程，由极坐标与直角坐标的互化公式，即可取得曲线的直角坐标方程；

    （2）由题意，求得直线的参数方程，代入椭圆的方程，利用参数的几何意义，即可求解。

    （1）由消去得，

    由得，即，

    故直线的普通方程为；曲线的直角坐标方程为：．

    （2）因为直线过，所以可设直线的参数方程为

    并代入椭圆的方程，整理得：，

    设，对应的参数为，，则，，且

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数的定义域为（）.

    （1）当时，求函数的值域；

    （2）若函数在定义域上是减函数，求的取值范围；

    （3）求函数在定义域上的最大值及最小值，并求出函数取最值时的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表：

    (1)求y关于x的线性回归方程；

    (2)利用(1)中的回归方程，当价格x＝40元/kg时，日需求量y的预测值为多少？

    参考公式：线性回归方程，其中＝，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，，令.

    （1）当时，求函数的单调区间及极值；

    （2）若关于的不等式恒成立，求整数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了调查某社区居民每天参加健身的时间，某机构在该社区随机采访男性、女性各50名，其中每人每天的健身时间不少于1小时称为“健身族”，否则称其为"非健身族”，调查结果如下：

    健身族

    非健身族

    合计

    男性

    40

    10

    50

    女性

    30

    20

    50

    合计

    70

    30

    100

    （1）若居民每人每天的平均健身时间不低于70分钟，则称该社区为“健身社区”. 已知被随机采访的男性健身族，男性非健身族，女性健身族，女性非健身族每人每天的平均健分时间分別是1.2小时，0.8小时，1.5小时，0.7小时，试估计该社区可否称为“健身社区”？

    （2）根据以上数据，能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关？

    参考公式： ，其中.

    参考数据：

    0. 50

    0. 40

    0. 25

    0. 05

    0. 025

    0. 010

    0. 455

    0. 708

    1. 321

    3. 840

    5. 024

    6. 635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2013年春节，有超过20万名广西、四川等省籍的外来务工人员选择驾驶摩托车沿321国道返乡过年，为保证他们的安全，交管部门在321国道沿线设立多个驾乘人员休息站，交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车，就进行省籍询问一次，询问结果如下图所示.

    （Ⅰ）问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法？

    （Ⅱ）用分层抽样的方法对被询问了省籍的驾驶人员进行抽样，若广西籍的有5名，则四川籍的应抽取几名？

    （Ⅲ）在上述抽出的驾驶人员中任取2名，求至少有一名驾驶人员是广西籍的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家电公司销售部门共有200位销售员，每位部门对每位销售员都有1400万元的年度销售任务，已知这200位销售员去年完成销售额都在区间（单位：百万元）内，现将其分成5组，第1组，第2组，第3组，第4组，第5组对应的区间分别为， ， ， ， ，绘制出频率分布直方图.

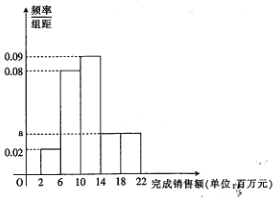
    （1）求的值，并计算完成年度任务的人数；

    （2）用分层抽样从这200位销售员中抽取容量为25的样本，求这5组分别应抽取的人数；

    （3）现从（2）中完成年度任务的销售员中随机选取2位，奖励海南三亚三日游，求获得此奖励的2位销售员在同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，圆与轴的一个交点为，圆的圆心为，为等边三角形.

    （1）求抛物线的方程

    （2）设圆与抛物线交于、两点，点为抛物线上介于、两点之间的一点，设抛物线在点处的切线与圆交于、两点，在圆上是否存在点，使得直线、均为抛物线的切线，若存在求点坐标（用、表示）；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查，得到的统计数据如表所示：

    积极参加班级工作

    不积极参加班级工作

    合计

    学习积极性高

    18

    7

    25

    学习积极性不高

    6

    19

    25

    合计

    24

    26

    50

    （1）如果随机调查这个班的一名学生，那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少？

    （2）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取2名学生参加某项活动，问2名学生中有1名男生的概率是多少？

    （3）学生的学习积极性与对待班级工作的态度是否有关系？请说明理由．

    附：

    查看答案和解析>>

    同步练习册答案