
【题目】已知函数![]()
(1)当![]() 时,设
时,设![]() ,讨论
,讨论![]() 的导函数
的导函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 上单调递减,
上单调递减,![]() 上单调递增;(2)
上单调递增;(2)![]()
【解析】
(1)当![]() 时,
时,![]() ,对导函数再次求导,转化成解一次不等式,从而得到
,对导函数再次求导,转化成解一次不等式,从而得到![]() 的单调区间;
的单调区间;
(2)由第(1)步的思路,构造函数![]()
![]() ,对函数进行求导后,再次求导得到
,对函数进行求导后,再次求导得到![]()
![]() ,对
,对![]() 分成
分成![]() 和
和![]() 两种情况进行讨论,先研究
两种情况进行讨论,先研究![]() 的单调性与函数值的正负,再研究
的单调性与函数值的正负,再研究![]() 的单调性与函数值的正负.
的单调性与函数值的正负.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,当
,当![]() ,当
,当![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)当![]() 时,
时,![]() ,令
,令![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
当![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
所以![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
所以![]() 在
在![]() 恒成立,
恒成立,
所以当![]() 时,不等式成立.
时,不等式成立.
②当![]() 时,
时,
当![]() ,当
,当![]() ,
,
所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
所以![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
所以![]() 在
在![]() 上恒成立,这与
上恒成立,这与![]() 相矛盾,
相矛盾,
所以![]() 不成立.
不成立.
综上所述:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)讨论函数![]() 的单调性.
的单调性.
(2)是否存在正实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() 时,值域也为
时,值域也为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率;
(2)根据统计数据估计图书分类错误的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为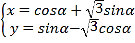 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某公司生产线生产的某种产品中抽取1000件,测量这些产品的一项质量指标,由检测结果得如图所示的频率分布直方图:
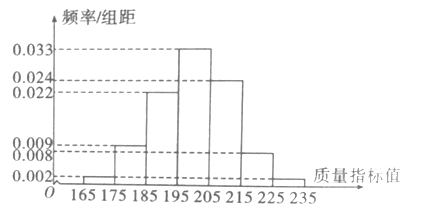
(1)求这1000件产品质量指标的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ⅱ)已知每件该产品的生产成本为10元,每件合格品(质量指标值![]() )的定价为16元;若为次品(质量指标值
)的定价为16元;若为次品(质量指标值![]() ),除了全额退款外且每件次品还须赔付客户48元.若该公司卖出10件这种产品,记
),除了全额退款外且每件次品还须赔付客户48元.若该公司卖出10件这种产品,记![]() 表示这件产品的利润,求
表示这件产品的利润,求![]() .
.
附:![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种规格的矩形瓷砖![]() 根据长期检测结果,各厂生产的每片瓷砖质量
根据长期检测结果,各厂生产的每片瓷砖质量![]() 都服从正态分布
都服从正态分布![]() ,并把质量在
,并把质量在![]() 之外的瓷砖作为废品直接回炉处理,剩下的称为正品.
之外的瓷砖作为废品直接回炉处理,剩下的称为正品.
(Ⅰ)从甲陶瓷厂生产的该规格瓷砖中抽取10片进行检查,求至少有1片是废品的概率;
(Ⅱ)若规定该规格的每片正品瓷砖的“尺寸误差”计算方式为:设矩形瓷砖的长与宽分别为![]() 、
、![]() ,则“尺寸误差”
,则“尺寸误差”![]() 为
为![]() ,按行业生产标准,其中“优等”、“一级”、“合格”瓷砖的“尺寸误差”范围分别是
,按行业生产标准,其中“优等”、“一级”、“合格”瓷砖的“尺寸误差”范围分别是![]() ,
,![]() 、
、![]() ,
,![]() 、
、![]() ,
,![]() (正品瓷砖中没有“尺寸误差”大于
(正品瓷砖中没有“尺寸误差”大于![]() 的瓷砖),每片价格分别为7.5元、6.5元、5.0元.现分别从甲、乙两厂生产的该规格的正品瓷砖中随机抽取100片瓷砖,相应的“尺寸误差”组成的样本数据如下:
的瓷砖),每片价格分别为7.5元、6.5元、5.0元.现分别从甲、乙两厂生产的该规格的正品瓷砖中随机抽取100片瓷砖,相应的“尺寸误差”组成的样本数据如下:
尺寸误差 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
频数 | 10 | 30 | 30 | 5 | 10 | 5 | 10 |
(甲厂瓷砖的“尺寸误差”频数表)用这个样本的频率分布估计总体分布,将频率视为概率.
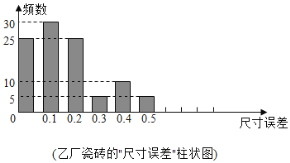
(ⅰ)记甲厂该种规格的2片正品瓷砖卖出的钱数为![]() (元
(元![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
(ⅱ)由如图可知,乙厂生产的该规格的正品瓷砖只有“优等”、“一级”两种,求5片该规格的正品瓷砖卖出的钱数不少于36元的概率.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ;
;![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com